Aurélie 03/02
solides en mouvement

Kiné Assas 2002

suite-->moteur électrique

Google

On considère le dispositif représenté par la figure ci-dessous. Un solide de masse m1 se déplace sans frottement sur le plan incliné d'un angle a =30°sur l'horizontale. Il est relié par un fil inextensible et de masse négligeable à un solide m2. Le fil ne glisse pas sur la poulie dont la masse est négligeable. Les frottements de l'air seront négligés.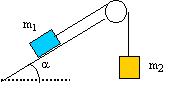

  1.  
  2. Reproduire le schéma sur la copie en y faisant apparaître les forces extérieures appliquées à chacun des deux solides m1 et m2.
  3. Calculer le rapport m1 / m2 pour que les solides soient en équilibre.
  4. En réalité m2 = 3 m1 et les solides sont abandonnés sans vitesse initiale.
    - Montrer que les solides se mettent en mouvement et préciser le sens du déplacement.
    -Calculer l'intensité a de l'accélération prise par chacun des deux solides.
    - Calculer l'intensité T de la tension du fil si m1 = 0,5 kg.
  5. Dans les conditions de la question 3, les deux solides s'étant déplacés de x= 15 cm après le lâcher, le fil se rompt brutalement.
    - Calculer l'énergie cinétique acquise par le solide m1 à l'instant de la rupture du fil.
    - Que devient alors la tension T du fil ?
    - En utilisant le théorème de l'énergie cinétique, calculer la distance d que le solide de masse m1 peut encore parcourir après la rupture du fil et avant de rebrousser chemin.

 

corrigé

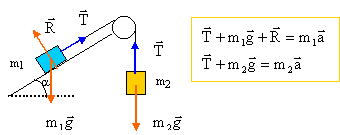
à l'équilibre la somme vectorielle des forces appliquées à m1 est nulle.

Projeter cette somme de vecteurs sur un axe parallèle au plan vers le haut : T-m1g sin a = 0

à l'équilibre la somme vectorielle des forces appliquées à m2 est nulle.

Projeter cette somme de vecteurs sur un axe vertical vers le haut : T-m2g = 0

d'où m2g = m1g sin a soit m2 = m1gsin a ; m1/m2=1/ sin 30 = 2 ou m1= 2 m2.

La seconde loi de Newton s'écrit pour m1, sur un axe parallèle au plan vers le haut :

T-m1g sin a = m1a (1)

de même pour m2 suivant un axe verticale vers le bas : m2g -T = m2a (2).

soit T = m2(g-a) ; repport dans (1) :

m2(g-a) -m1g sin a = m1a soit a = g(m2-m1 sin a ) / (m1+m2).

si m2> m1 sin a ( m2 > 0,5 m1) alors m1 monte le plan et m2 descend.

application numérique : m2 = 3m1.

a = 9,8 ( 3m1 - 0,5 m1) / (4m1) = 6,125 m/s².

T= m2(g-a) = 1,5*(9,8-6,125) = 5,51 N.

Le fil casse : la tension s'annule.

v² fin - v² départ = 2 a x soit : v² fin - 0 = 2 a x = 2*6,125*0,15 = 1,84 m²/s²

énergie cinétique aquise par m1 : Ec = ½m1v²fin = m1 a x

Ec = 0,5*6,125*0,15 = 0,46 J.

distance d'arrêt notée d :

théorème de l'énergie cinétique: départ ( le fil casse) fin :( arrêt)

seul le poids travaille car l'action du support est perpendiculaire au plan.

travail du poids résistant dans une montée : - m1 g sin a .

½ m1v² fin - ½ m1 v² départ = - m1 g d sin a .

0 - ½ m1 v² départ = - m1 g d sin a .

d = 0,5 v² départ / ( g sin a ) = 0,5*1,84 / (9,8*0,5)= 0,19 m.

retour - menu