Aurelie 02/ 02
solide sur un plan incliné

Concours kiné Assas 01

suite --> auto-induction et transfert d'énergie

Google

Un solide (S) de centre d'inertie G et de masse m peut se déplacer sur un plan incliné faisant un angle a avec l'horizontale. Un dispositif d'enregistrement relié à un ordinateur permet de repérer les positions du centre d'inertie G et de mesurer sa vitesse instantanée à chaque instant. Le solide est lâché sans vitesse initiale d'un point O du plan et son mouvement suit la ligne de plus grande pente dont la direction est notée Ox. La position du point G est repérée par son abscisse dans le repère (O ; i). L'action des forces de frottement peut être assimilée à celle d'une force constante f, de même direction mais de sens contraire au vecteur vitesse.

Le dispositif d'enregistrement est déclenché à l'instant t0=0 et donne les positions xA et xB de G et les vitesses vA et vB aux instants tA et tB.
temps (s)
position (m)
vitesse (m/s)
point A
0,3
0,18
0,57
point B
0,7
0,48
0,929

  1. Faire l'inventaire des forces s'appliquant au solide (S) et les représenter sur un schéma.
  2. En utilisant le th. de l'énergie cinétique entre les positions A et B, exprimer l'intensité f de la force de frottement en fonction de m, g, a, xA, xB, vA, vB. Calculer la valeur numérique de f.
  3. Calculer le travail mécanique effectué par la force de frottement entre les points A et B. Que signifie le signe de la valeur trouvée ?. Quelle forme d'énergie voit on apparaître ?
  4. Exprimer l'intensité de l'accélération a du point G au cours du mouvement en fonction de m, g, a et f.. Calculer la valeur numérique de a.
  5. A l'instant t=0, la position du centre d'inertie est repérée par son abscisse x0 et sa vitesse a pour mesure v0.
    - Donner les équations horaires x(t) et v(t) du mouvement du centre d'inertie G du solide dans le repère (O ; i).
    - Calculer les valeurs numériques de la position x0 et de la vitesse v0 du centre d'inertie G du solide au moment où l'enregistrement est déclenché.

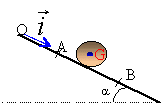
m =200g ; a=30°  

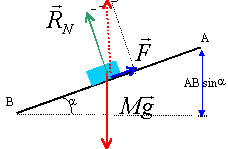
corrigé
le solide est soumis à son poids, vertical vers le bas, à l'action du plan décomposée en une action normale au plan Rn et en une action parallèle au plan F , de sens contraire à la vitesse.

les vecteurs sont écrits en bleu et en gras.

thèorème de l'énergie cinétique :

travail du poids entre A et B ( descente: donc travail moteur )

W1 = mg(hA-hB) = mgABsin a =mg(xB-xA) sin a .

travail résistant des frottements :

W2 = -F AB = - F(xB-xA)

Rn perpendiculaire à la vitesse ne travaille pas.

variation d'énergie cinétique : DEc = ½ mV²fin -½ mV²départ = ½ mV²B -½ mV²A

La variation d'énergie cinétique est égale à la somme des travaux des forces.

½ mV²B -½ mV²A= mg(xB-xA) sin a- F(xB-xA)

F = m[gsin a - ½(V²B -V²A) / (xB-xA)]

F = 0,2[ 9,8 sin 30-½(0,929²-0,57²) / (0,48-0,18)] = 0,8 N.

travail des frottements :

W2 = -F AB = - F(xB-xA) = -0,8(0,48-0,18) = -0,24 J.

le signe moins signifie : diminution de l'énergie mécanique du système {solide-terre}

cette énergie perdue se retrouve sous forme d'énergie thermique dans l'environnement.

accélération :

la seconde loi de Newton s'écrit : P + F + Rn = m a

soit sur l'axe O,i : mg sina -F = ma

a = g sin a-F / m.

a = 9,8 sin 30 - 0,8 / 0,2 = 0,9 m/s².

équation horaire :

vitesse : v = a t + v0 = 0,9 t + v0 .

0,57 = 0,9 *0,3 + v0 d'où v0 = 0,3 m/s.

abscisse : primitive de la vitesse

x = ½ at² + v0 t + x0 = 0,45 t² + 0,3 t + x0.

0,48 = 0,45*0,7² + 0,3*0,7 + x0 d'où x0 = 0,05 m.
retour - menu