Aurélie nov 2001
Précipitation

sulfates des métaux alcalino-terreux

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

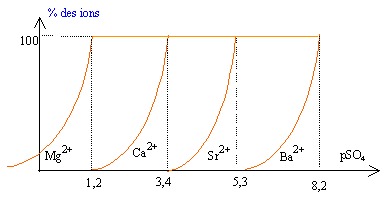
Dans 1 L d'eau pure on introduit 7,624 g de chlorure de magnésium, 6,666 g de chlorure de calcium, 6,344 g de chlorure de strontium et 4,166 g de chlorure de baryum. La solution n'est pas saturée.

On donne : Mg= 24,3 ; Ca= 40,1 ; SR= 87,6 ; Ba= 137,3 ; Cl = 35,5 g/mol
On y ajoute alors progressivement une solution d'acide sulfurique à 1 mol/L.

Diagramme théorique de distribution des espèces :

 

  1. Calculer les produits de solubilité des différents ions Ba2+, Ca2+, Mg2+, Sr2+ en présence d'ion sulfate.
  2. Quels sont les volumes d'acide sulfurique faisant apparaître successivement les précipités.
  3. Dés que le sulfate de strontium sprécipite, quelle est la concentration des ions baryum ?
  4. Quelle est l'application de ces précipitations successives ?
corrigé
On note X2+ l'un quelconque des ions Ba2+, Ca2+, Mg2+, Sr2+

Le produit de solubilité s'écrit : Ks = [X2+] [SO42- ]

ou encore log Ks = log [X2+] + log[SO42- ]

-pKs = log [X2+] -pSO4.

pKs = -log [X2+] + pSO4.


MgCl2
CaCl2
SrCl2
BaCl2
masse molaire (g/mol)
95,3
111,1
158,6
208,3
concentration

[X2+] mol/L
7,624 / 95,3

= 0,08
6,666 / 111,1

= 0,06
6,344 / 158,6

= 0,04
4,166 / 208,3

= 0,02
-log [X2+]
1,1
1,22
1,40
1,7


MgSO4
CaSO4
SrSO4
BaSO4
pKs
1,1+1,2= 2,3
1,22+3,4 = 4,62
1,4+5,3= 6,7
1,7 + 8,2 = 9,9
Ks= 10-pKs
5 10-3
2,4 10-5
2 10-7
1,26 10-10
Les précipités apparaissent dans l'ordre croissant des produits de solubilité

soit dans l'ordre BaSO4 ;  SrSO4 ; CaSO4 ; MgSO4

volume de la solution acide :

Au début de la précipitation du sulfate de baryum [SO42- ] = 10-8,2 = 6,3 10-9 mol/L

on a alors verdé v1 L de solution d'acide sulfurique

[SO42- ] = Qté matière (mol) / volume total solution (L) = 1*v1 / (1+v1)

6,3 10-9(1+v1)= v1d'où v1 = 6,3 10-9 L , précipitation immédiate.

Au début de la précipitation de SrSO4 :

[SO42- ] [Ba2+]= 1,26 10-10 donne [SO42- ] = 1,26 10-10 / [Ba2+]

et [SO42- ] [Sr2+]= 2 10-7donne [SO42- ] = 2 10-7 / [Sr2+]

soit 1,26 10-10[Sr2+] = 2 10-7[Ba2+]

[Sr2+] = 1587 [Ba2+]

on a ajouté v2 L d'acide sulfurique :

[Sr2+] =0,04 / (1+v2) et [Ba2+] = (0,02-v2)/ (1+v2)

0,04 = 1587 (0,02-v2) d'où v2 = 0,02 L.

Au début de la précipitation de CaSO4 :

[SO42- ] [Ca2+]= 2,4 10-5 donne [SO42- ] = 2,4 10-5 / [Ca2+]

et [SO42- ] [Sr2+]= 2 10-7donne [SO42- ] = 2 10-7 / [Sr2+]

soit 2,4 10-5 [Sr2+] = 2 10-7[Ca2+]

[Ca2+] = 120 [Sr2+]

on a ajouté v3 L d'acide sulfurique :

Qté de matière (mol) d'ion Sr2+ ayant précipité : (v3-v2 )1 mol

[Ca2+] =0,06 / (1+v3) et [Sr2+] = (0,04-(v3-v2 ))/ (1+v3)

0,06 = 120 (0,04-(v3-v2 )) d'où v3 -v2 = 39,5 mL et v3 = 59,5 mL.

Au début de la précipitation de MgSO4 :

[SO42- ] [Ca2+]= 2,4 10-5 donne [SO42- ] = 2,4 10-5 / [Ca2+]

et [SO42- ] [Mg2+]= 5 10-3donne [SO42- ] = 5 10-3 / [Mg2+]

soit 2,4 10-5 [Mg2+] = 5 10-3[Ca2+]

[Mg2+] = 208 [Ca2+]

on a ajouté v4 L d'acide sulfurique :

Qté de matière (mol) d'ion Ca2+ ayant précipité : (v4-v3 )1 mol

[Mg2+] =0,08 / (1+v4) et [Ca2+] = (0,06-(v4-v3 ))/ (1+v4)

0,08 = 208 (0,06-(v4-v3 )) d'où v4 -v3 = 59,6 mL et v4 = 119,1 mL.

[Ba2+] lorsque SrSO4 commence à précipiter :

Au début de la précipitation du sulfate de strontium [SO42- ] = 10-5,3 = 5 10-6 mol/L

[SO42- ] [Ba2+]= 1,26 10-10 donne [Ba2+] =1,26 10-10 / 5 10-6 = 2,52 10-5 mol/L. négligeable.

Lorsque les différents précipités apparaissent les ions en solution correspondant aux précipités restent ultra minoritaires.

On peut donc faire une séparation par précipitation ; on élimine les précipités successifs par filtration

 

retour - menu