Charge d'un condensateur : dipôle RC ; générateur de tension, générateur de courant. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

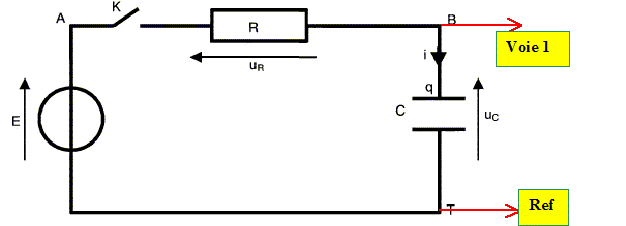
On dispose de deux composants : un conducteur ohmique de résistance R = 150 W et un condensateur de capacité C inconnue. On étudie la charge du condensateur à travers le conducteur ohmique à l'aide d'un générateur de tension de f.e.m. E = 5,1 V. Faire le schéma du montage en indiquant les branchements nécessaires pour suivre l'évolution de la tension uC(t) aux armatures du condensateur en fonction du temps. 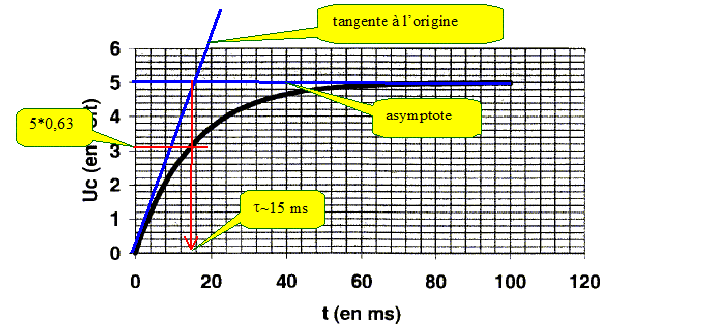Constante de temps : On suppose le condensateur déchargé. A l'instant t = 0, on ferme l'interrupteur K. Le phénomène observé est caractérisé par une grandeur appelée constante de temps notée t. Que signifie l'expression " phénomène caractérisé par t " ? La constante de temps permet d'estimer la durée de la charge du condensateur : cette durée est voisine de 5 fois la constante de temps. A l'aide d'une courbe, estimer l'ordre de grandeur de t sans aucun calcul. . . Ordre de grandeur de la constante de temps 10 ms ou 10-2 s. Quelle est l'expression de t en fonction des caractéristiques des composants du circuit ? t = RC. Vérifier que l'expression précédente est homogène à un temps. R résistance soit tension / intensité ; C capacité soit charge / tension d'où on déduit : RC charge / intensité or une charge est une intensité fois un temps ; par suite RC a la dimension d'un temps. Equation différentielle vérifiée par uC(t) : Les conventions de sens et d'orientation pour le courant et les tensions sont indiquées sur le schéma du montage. Ecrire la relation qui existe entre E, uR et uC. Additivité des tensions : uR + uC =E. Exprimer uR en fonction de l'intensité i du courant. uR = R i. Rappeler l'expression de i en fonction de q, charge portée par l'armature reliée au point B du circuit. i = dq/dt. Rappeler l'expression de q en fonction de uc. En déduire celle de i en fonction de uC. q= Cuc ; i = Cduc /dt. En utilisant les résultats précédents montrer que la tension aux armatures du condensateur uC(t) vérifie l'équation différentielle : t duc /dt+uc = E (1) uR + uC =E s'écrit : Ri + uC =E ; RCduc /dt + uC =E ; t duc /dt + uc = E.       Web www.chimix.com Propriétés de la fonction uc(t) : Vérifier que uC(t) = E.[1-exp(-t/t ] est solution de l'équation différentielle précédente et satisfait à la condition initiale : t = 0, condensateur déchargé. uC(t) = E.[1-exp(-t/t )] ; duc /dt = E /t exp(-t/t) ; repport dans (1) : t E /t exp(-t/t) +E.[1-exp(-t/t )] = E E exp(-t/t) +E -E exp(-t/t) =E est vérifié quel que soit t. De plus à t=0 : uC(0) =E[1-exp(-0/t )] = E(1-1) = 0, le condensateur est initialement déchargé. Déterminer la valeur du rapport uC/E à la date t = t. uC/E = 1-exp(-1) = 0,63. En utilisant ce résultat et en exploitant la courbe, déterminer la valeur de t puis celle de C. t=15 ms = 15 10-3 s( lecture graphe) ; t =RC avec R=150 W d'où C = 15 10-3 / 150 = 1,0 10-4 F.   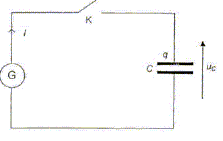Charge du condensateur à courant constant.       A la date t0 = 0 s, on ferme l'interrupteur K et on débute l'enregistrement informatisé des variations de la tension aux bornes du condensateur uC(t) en fonction du temps. 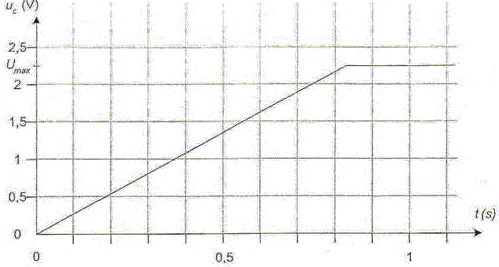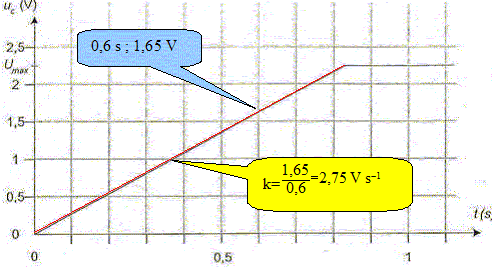On obtient le graphe suivant : Nommer les deux régimes observables sur le graphe uC = f(t) représenté ci-dessus. De 0 à 0,84 s, le condensateur initialement déchargé, se charge, la tension à ses bornes croît. De 0,84 s et au delà, le condensateur est chargé, la tension à ses bornes reste constante. Donner l'expression de uC en fonction de C et de la charge q du condensateur. La charge q et la tension uC aux bornes du condensateur sont proportionnelles : la constante de proportionalité est la capacité C. q= Cuc soit uc=q/C. (1) Le condensateur est initialement déchargé. Donner l'expression de la charge du condensateur q en fonction de l'intensité I et de la date t lorsque uC est inférieure à Umax (charge à courant constant). L'intensité étant constante la cgarge q et l'intensité sont proportionnelles. q=It. (2) En déduire que uC =I t/C tant que uC est inférieure à Umax. (1) et (2) conduisent à : Cuc= It soit uc=I/C t. (3) Déterminer la valeur et préciser l'unité du coefficient directeur, noté k, de la portion de droite de la figure ci-dessus lorsque uC est inférieure à Umax . Utiliser ce résultat pour vérifier que la valeur de C est compatible avec les indications du constructeur. k = I/C avec I = 0,27 A ; C =I/k = 0,27/2,75 = 9,8 10-2 F. Le constructeur indique 0,1 F à + ou - 10% près soit C comprise entre 0,09 et 0,11 F. Il y a donc compatibilité entre la valeur déterminée ci-dessus et l'indication du constructeur.

retour -menu