Radioactivité, loi de décroissance, constante de temps, demi-vie. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Définir les termes suivants : noyaux isotopes : deux isotopes ne se différencient que par leur nombres de neutrons ; ils ont le même numéro atomique. fission nucléaire : un noyau "lourd" instable se casse en deux noyaux plus petits lors du choc avec un neutron ; cette réaction libère beaucoup d'énergie. demi-vie : durée au bout de laquelle l'activité initiale est divisée par 2 ; durée au bout de laquelle le nombres de noyaux radioactifs initiaux et divisé par 2. Définir un noyau radioactif. Un noyau radioactif est instable : il se désintègre spontanément, de manière aléatoire mais inéluctable, en donnant un noyau " fils", plus stable. Cette réaction s'accompagne de libération d'énergie et de l'émission d'autres particules. Préciser le nombre de masse et le numéro atomique de chacune des deux particules, neutron et b-. 10n : un neutron n'a pas de charge, il est constitué d'un nucléon. b- : 0-1e électron négatif, pas de nucléon. Déterminer les valeurs de x et de y dans l'équation. 23892U + x10n --> 24194Pu + y 0-1e Conservation du nombre de la charge :  92+0 = 94-y d'où y=2. Conservation du nombre de nucléons : 238+x=241 d'où x = 3.  23892U + 310n --> 24194Pu + 2 0-1e La mesure de l'activité du radon dans une cave a donné un résultat de 6000 Bq par m3 d'air. Un noyau radioactif peut être caractérisé par sa constante radioactive l. L'activité d'un échantillon radioactif à un instant t, notée A(t) est liée au nombre de noyaux radioactifs N(t) dans l'échantillon au même instant par la relation : A(t)= l N(t) La demi-vie radioactive t½est liée à la constante radioactive l par la relation l t½ = ln2 Calculer la valeur de l pour le radon 222. Sa demi-vie radioactive est : 3,82 jours = 3,82*24*3600 =3,30 105 s. l= ln2 / t½ = 0,693 / 3,30 105=2,10 10-6 s-1. Quelle est la masse de radon 222 contenue dans 1,0 m3 d'air de cette cave ? N(t) = A(t)/ l =6000/2,10 10-6 =2,856 109 noyaux dans un m3 d'air. Quantité de matière de radon : n = N(t) / NA =2,856 109 / 6,02 1023 =4,745 10-15 mol m-3. Masse de radon : m = n M = 4,745 10-15 *222 = 1,05 10-12 g par m-3. La loi de décroissance de l'activité en fonction du temps est A(t) = A0 exp(-lt). En supposant que le radon ne s'infiltre plus et ne s'échappe pas de cette cave, au bout de combien de jours l'activité du radon 222 serat-elle de 400 Bq m-3 ? On exprime la constante radioactive en jour-1 : l = ln2 / t½ = 0,693/3,82 = 0,1814 jour-1. ln(A0/A) = lt ; t = ln(A0/A) / l= ln(6000/400) / 0,1814 = 14,9 jours. Quelles mesures imples faut-il prendre pour diminuer la concentration en radon de cette cave ? 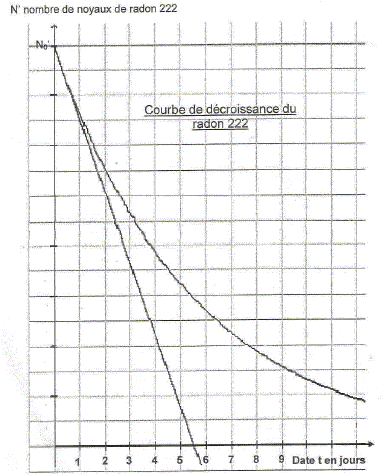"aérer et ventiler les maisons, les sous sols et les vides sanitaires ; améliorer l'étanchéité des murs et des planchers."      Web www.chimix.com Le radon 222 a pour temps de demi-vie 3,8 jours. Le radon 222 produit par la désintégration du radium 226 est lui même radioactif a.   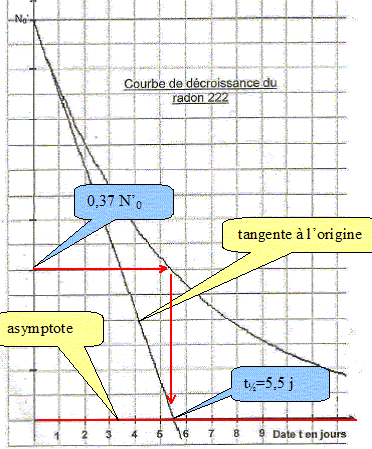Déterminer graphiquement la constante de temps t. Préciser la méthode utilisée. Rappeler la définition du temps de demi-vie t½. Etablir son expression en fonction de la constante de temps t puis calculer le temps de demi-vie. La valeur calculée est-elle en accord avec la valeur donnée ? Temps de demi-vie : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés. Loi de décroissance radioactive : N(t) = N0 exp(-lt) = N0 exp(-t/t) . 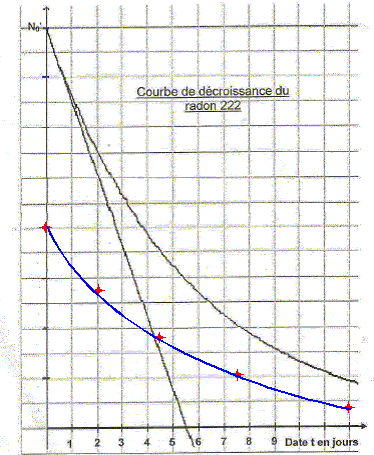On identifie : t = 1/l N(t½) = 0,5 N0 = N0 exp(-lt½) ; ln0,5 = -lt½ ; ln2 = lt½ = t½ /t. t½ = t. ln2 = 5,5*0,693 =3,8 jours. ( accord avec la valeur donnée) Construire sur le même graphique, en utilisant les mêmes échelles, la courbe représentant la loi de décroissance du radon 222 pour un nombre initial de noyaux deux fois plus faible.

retour -menu