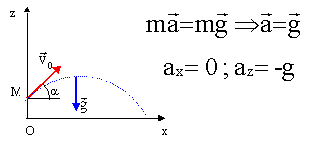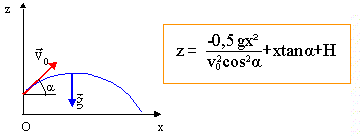Aurélie 12/06/07
 

Projectile, le trébuchet bac S 2007 La Réunion

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. 
. .
.
.

Sans calculatrice ; 5,5 pts ; d'autres corrigés labolycee.org ; intellego.fr ; montblancsciences.free.fr.

Le trébuchet est une machine de guerre utilisée au Moyen Age au cours des sièges de châteaux forts. Le projectile pouvait faire des brèches dans les murailles des châteaux forts situés à plus de 200 m du trébuchet. Son principe de fonctionnement est le suivant :

Un contrepoids relié à un levier est maintenu à une certaine hauteur par des cordages. Il est brusquement libéré. Au cours de sa chute, il agit sur un levier au bout duquel se trouve une poche en cuir dans laquelle est placé le projectile.

Lors de sa libération, le projectile de la poche se trouve à une hauteur H = 10 m et est projeté avec une vitesse faisant un angle a avec l'horizontale

Les mouvements du contrepoids et du projectile s'effectuent dans un champ de pesanteur uniforme.

Données : Masse du projectile m = 130 kg ; g = 10 m/s² ; H = 10 m ;masse volumique de l'air rair = 1,3 kg.m -3 ; volume du projectile V = 50 L.

Étude du mouvement du projectile après libération

Le système étudié est le projectile. Les frottements de l'air sur le projectile seront négligés dans cette étude. Le champ de pesanteur est parallèle à l'axe Oz.

  1. Donner les caractéristiques (sens, direction et valeur) du poids et de la poussée d'Archimède qui s'exercent sur le projectile.
  2. Est-il judicieux de négliger par la suite la poussée d'Archimède ?
  3. En appliquant la 2ème loi de Newton dans le cadre de la chute libre, déterminer les coordonnées ax et az du vecteur accélération du centre d'inertie du projectile dans le repère indiqué.
  4. Donner l'expression des coordonnées du vecteur vitesse initiale v0 , notées v0x et v0z , en fonction de v0 et a.
  5. On appelle vx(t) la composante horizontale du vecteur vitesse et vz(t) sa composante verticale. Déterminer l'expression des composantes horizontale et verticale vx(t) et vz(t) du vecteur vitesse du système au cours de son mouvement.
  6. En déduire la nature du mouvement du projectile en projection sur l'axe horizontal. Justifier.
  7. Déterminer l'expression des équations horaires du mouvement du projectile : x(t) et z(t).
  8. Montrer que l'équation de la trajectoire du projectile est la suivante :z= -½ g x2/ ( v0 cos a)2 + x tan a + H.
  9. Quelle est la nature de la trajectoire du projectile ? Représenter qualitativement l'allure de la trajectoire.
  10. En utilisant l'expression de l'équation de la trajectoire, indiquer les paramètres de lancement qui jouent un rôle dans le mouvement du projectile.
  11. Dans le cas où le projectile est lancé avec une vitesse initiale horizontale, montrer que l'abscisse de son point de chute est : x = v0 ( 2H/g)½.
  12. Avec quelle vitesse initiale v0 horizontale, le projectile doit-il être lancé pour atteindre la base du mur du château situé à une distance x = 100 m ?
Aide au calcul : 0,5½ = 0,71 ; 2½ = 1,41.

.
.

Le poids :

Appliqué au centre d'inertie du boulet, vertical, dirigé vers le bas, valeur P=mg = 130*10 = 1,3 103 N.

La poussée d'Archimède :

Appliquée au centre d'inertie du boulet, verticale, dirigée vers le haut;

Sa valeur est égale au poids du volume d'air déplacé : PA= V rair g

avec V= 50 L = 0,050 m3 ; rair = 1,3 kg.m -3 ; g = 10 m/s².

PA = 0,050*1,3*10 = 0,65 N.

La valeur de la poussée d'Archimède étant environ 2000 fois plus petite que la valeur du poids, la poussée peut être négligée devant le poids.

Coordonnées ax et az du vecteur accélération du centre d'inertie du projectile :

Appliquer la 2ème loi de Newton dans le cadre de la chute libre.

Coordonnées du vecteur vitesse initiale v0 :

v0x = v0 cos a ; v0z =v0 sin a.

On appelle vx(t) la composante horizontale du vecteur vitesse et vz(t) sa composante verticale.

Composantes horizontale et verticale vx(t) et vz(t) du vecteur vitesse du système au cours de son mouvement :

Le vecteur vitesse est une primitive du vecteur accélération :

vx(t) = v0 cos a ; vz(t) = -gt + v0 sin a.

Nature du mouvement du projectile en projection sur l'axe horizontal :

La valeur de la composante horizontale de la vitesse est constante : le mouvement est donc uniforme suivant Ox.

Equations horaires du mouvement du projectile : x(t) et z(t).

Le vecteur position est une primitive du vecteur vitesse :

x(t) = v0 cos a t (1)

z(t) = -½gt2 + v0 sin a t + H. (2)

Equation de la trajectoire du projectile est la suivante :

(1) donne t = x / v0 cos a. Repport dans (2).

z = -½ g x2/ ( v0 cos a)2 + x tan a + H.

Nature de la trajectoire du projectile : arc de parabole.

 

 

Les paramètres de lancement qui jouent un rôle dans le mouvement du projectile sont la vitesse initiale v0, l'angle a et l'altitude initiale H.

Dans le cas où le projectile est lancé avec une vitesse initiale horizontale, l'abscisse de son point de chute est

Dans l'expression de z, écrire que a =0 , c'est à dire cos a =1 et tan a = 0 :

z = -½ g x2/ v02 + H.

L'altitude du point de chute étant nulle : -½ g x2/ v02 + H = 0

x2 =v02 2H / g ; x= v0 ( 2H/g)½.

Pour atteindre la base du mur du château situé à une distance x = 100 m, le projectile doit être lancé avec une vitesse initiale horizontale v0 de :

v02 = x2 g /(2H) ; v0 = x (g/(2H))½.

v0 = 100 (10/20)½ = 100*0,5½ = 100*0,71 = 71 m/s.
 
retour -menu