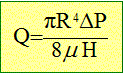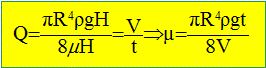|
Etude du comportement rhéologique d'une huile végétale pure BTS chimiste 2007 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
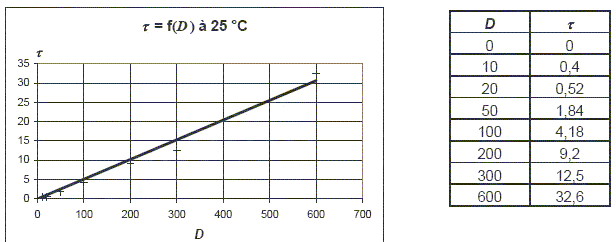
Définir les grandeurs ( et leur unité ) définies en abscisse et ordonnée. t : contrainte de cisaillement exprimée en pascal (Pa) D : vitesse de déformation ( seconde-1). Choisir, parmi les trois
adjectifs suivants, celui qui est le plus approprié
pour définir le comportement du fluide
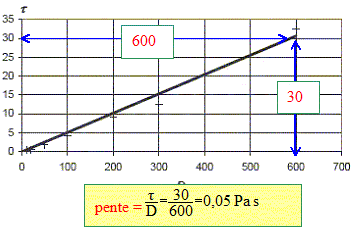
: Le rhéogramme est une droite donc comportement newtonien. Détreminer l'équation de cette courbe; quelle grandeur physique est représentée par la pente ? La pente de la droite correspond à la viscosité dynamique ( Pa s)
t = 0,05 D
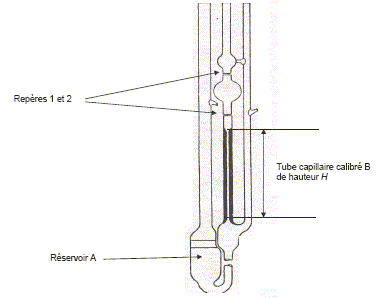
Etude de la viscosité dynamique d'une huile végétale pure en fonction de la température. On utilise un viscosimètre de type Ubbelöhde en verre indilatable dont le schéma est le suivant :
Ce viscosimètre contient un tube capillaire calibré B placé verticalement dans une cuve thermostatée. On introduit le fluide à étudier dans le réservoir A, et on mesure le temps que met le volume V de fluide contenu entre les repères 1 et 2 pour s'écouler à travers le capillaire. L'écoulement du fluide se fait sous une différence de pression constante DP due à la seule hauteur hydrostatique du fluide dans le capillaire. L'écoulement du fluide se fait à une température uniforme, fixée grâce au bain thermostaté. La loi d'écoulement dans les capillaires est la suivante :
Q est le débit volumique du fluide, R et H respectivement le rayon et la longueur du tube capillaire ; m la viscosité dynamique et DP la différence de pression existant entre les deux extrémités du tube capillaire. Cette expression est valable pour un fluide incompressible en écoulement laminaire permanent.
Un fluide est "incompressible" si sa
masse volumique est
constante à tempérture
constante. Dans certains écoulements, les particules
diffusent très lentement : elles
s’écartent peu les unes des autres. Les différentes couches du fluide
glissent les unes par rapport les autres : elles ne
se mélangent pas L’écoulement est dit
laminaire. Exprimer DP en utilisant les notations de l'énoncé. On note g=9,81 l'accélération de la pesanteur. DP est due à la seule hauteur hydrostatique H du fluide dans le capillaire : DP = rgH. Rappeler la relation entre le débit volumique Q et V, volume du fluide écoulé entre les deux traits du réservoir pendant le temps t. Q= V/t. Exprimer m en fonction de V, t, R4, r et g.
Préciser les grandeurs physiques, mesurées dans les conditions de l'expérience, dépendant de la température dans l'expression de m. Le verre du capillaire est indilatable: R et V indépendants de la température. La masse volumique du fluide dépend de la température. La durée de l'écoulement dépend de la température.
La première mesure t1 de temps d'écoulement se fait à la température T1=298 K. Exprimer m1 à cette température. m1 = A r1t1 avec A= pR4g / (8V) = constante. La seconde mesure t2 de temps d'écoulement se fait à la température T2. Exprimer m2 à cette température. m2 = A r2t2 avec A= pR4g / (8V) = constante. Donner l'expression du rapport m2 /m1 et en déduire une relation de la forme m2 = K r2 t2. Exprimer K. m2 /m1 = r2t2 / ( r1t1) = K r2 t2 si K = 1/(r1t1) Calculer la valeur
numérique de K à partir du tableau ci-dessous
: K = 1/(915*443,1)=2,47 10-6 m3 kg-1 s-1. ( 2,4665)
Compléter le tableau.
Montrer que le comportement de cette huile végétale pure en fonction de la température peut être modélisée par la relation m = A exp(B/T). ln m = ln A + B/T On trace la courbe : ln m = f(1/T)
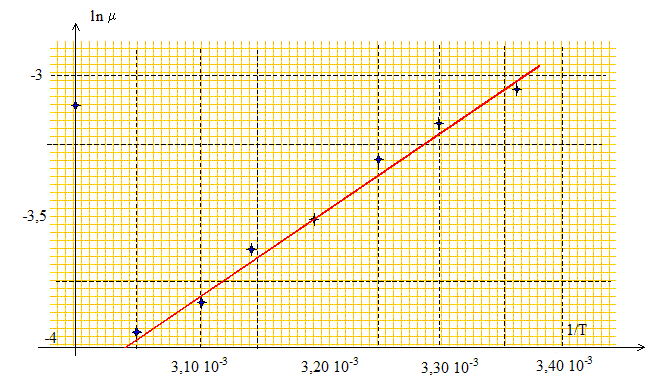
La courbe est une droite : le modèle m = A exp(B/T) est correct. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||