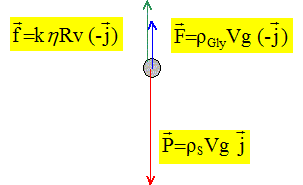Chute d'une bille dans un liquide. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

On réalise l'expérience suivante : Un long tube OS, fermé aux deux extrémités, contient du glycérol de viscosité h et une bille en acier. Le tube est retourné à l'instant t=0, la bille se trouve alors en haut du tube, sans vitesse initiale puis elle tombe verticalement dans le glycérol. g= 9,81 m s-2 ; d=OS= 40 cm. Deux traits horizontaux ont été tracés en D et F. Masse volumique de l'acier rS=7850 kg m-3. Rayon de la bille : R= 6,0 10-3 m ; volume de la bille V. Masse volumique du glycérol rgly=1260 kg m-3. La viscosité h s'exprime en Pa.s L'étude est effectuée dans le référentiel du laboratoire supposé galiléen. Les vecteurs sont écrits en gras et en bleu. Les forces. Donner l'expression vectorielle du poids P en fonction de rS, V, g et j. Valeur du poids : P= mg avec masse(kg) = volume (m3) * masse volumique ( kg m-3) ; m= VrS. Donner l'expression vectorielle de la poussée d'Archimède F en fonction de rgly, V, g et j. Poids du volume de glycérol déplacé, verticale, vers le haut.  L'intensité de la force de frottement, a pour expression f = khRv ; v est la valeur de la vitesse de chute de la bille, k est une constante sans dimension. Donner l'expression vectorielle de la force de frottement f.  Verticale, vers le haut. Représenter ces forces sur un schéma sans souci d'échelle.     . .   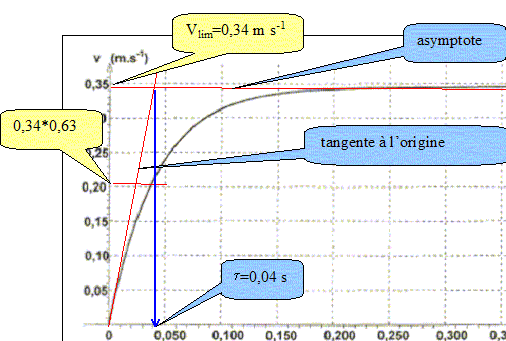Web www.chimix.com Détermination de la viscosité du glycérol : principe du viscosimètre. Au cours de la chute, la bille atteint très rapidement sa vitesse limite, notée vlim. Lorsque la bille passe devant le trait D et au delà, sa vitesse est constante. La durée de la chute Dtch de la bille entre les deux traits D et F qui sont distants d'une hauteur L, est mesurée. Exprimer la vitesse limite en fonction de Dtch et L.  Le mouvement de la bille est rectiligne uniforme : vlim = L / Dtch. Ecrire la relation vectorielle entre les forces s'exerçant sur la bille lorsqu'elle se trouve entre les deux traits D et F. Justifier la réponse. Le mouvement de la bille étant rectiligne uniforme, le principe d'inertie indique que la bille est pseudo-isolée ( la somme vectorielle des forces est nulle).  (1) En déduire l'expression de la viscosité du glycérol h = C(rS-rgly) Dtch avec C= Vg/(kRL). (1) donne : (rS-rgly)Vg = khRvlim ; h = (rS-rgly)Vg / (kRvlim ) h = (rS-rgly)Vg Dtch / (kRL ) = C(rS-rgly) Dtch Calculer la valeur de h si C= 7,84 10-4 m2s-2 et Dtch = 0,29 s. h = 7,84 10-4(7850-1260)*0,29 = 1,5 Pa .s. 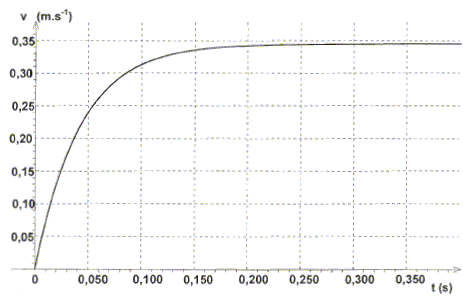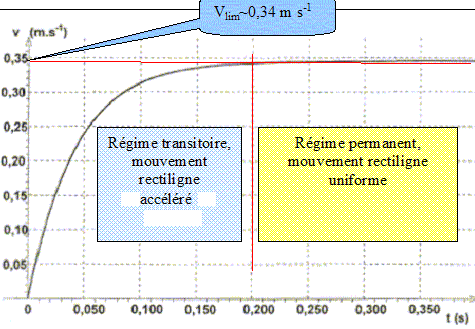tude du mouvement de la chute de la bille. Le début de la chute est filmé, puis le traitement de la vidéo a permis d'obtenir la représentation de la vitesse de la bille en fonction du temps. 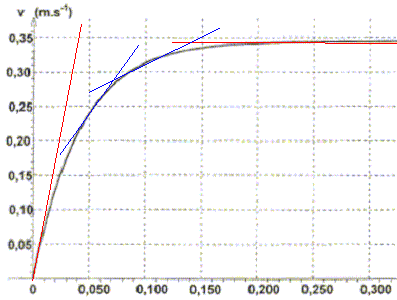Identifier les deux phases d'évolution de la vitesse et les nommer. Déterminer graphiquement le temps caractéristique t de l'évolution de la valeur de la vitesse de la bille et la vitesse limite vlim atteinte par la bille.   Comment le graphe v(t) permet-il d'étudier l'évolution de l'accélération au cours du temps ? Décrire cette évolution. L'accélération est la dérivée de la vitesse par rapport au temps. A une date donnée, tracer la tangente à la courbe v(t) : son coeficient directeur donne l'accélération à la date t. 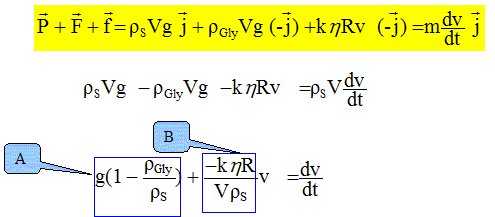Au cours du temps les tangentes se rapprochent de l'horizontale : les coefficients directeurs diminuent jusqu'à s'annuler lorsque le régime permanent est atteint. Par application de la seconde loi de Newton, établir l'équation différentielle vérifiée par la vitesse de la bille. L'écrire sous la forme dv/dt = A+Bv. Calculer A et préciser son unité. A = 9,81(1-1260/7850) =8,24 m s-2. En déduire la valeur de l'accélération a0 de la bille à t=0. A t=0, la vitesse initiale est nulle et l'équation différentielle s'écrit : [dv/dt]0 = A = a0 = 8,24 m s-2.

retour -menu