Propriétés d'une solution d'ammoniac bac S Inde 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

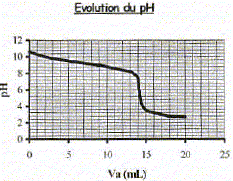
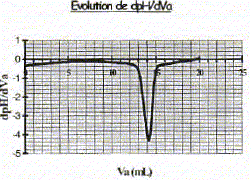
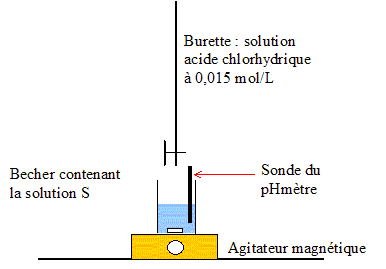
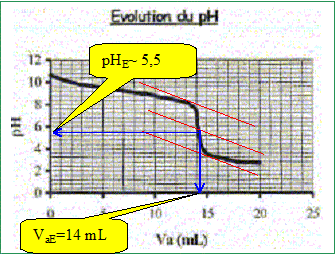
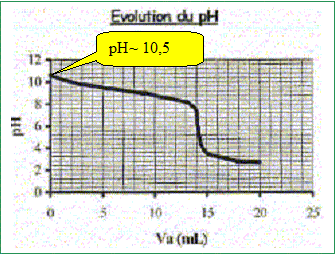
Données : Produit ionique de l'eau : Ke = 1,0.10-14. pKa des couples acide/base : H3O+(aq) / H2O( l) : pKa1 = 0 NH4+(aq) / NH3(aq) : pKa2 = 9,2 ; H2O(l ) / HO-(aq) : pKa3 = 14 Une solution commerciale S0 d'ammoniac NH3(aq) de concentration C0 = 1,1 mol.L-1 peut être utilisée, après dilution, comme produit nettoyant (éviers, lavabos, …) ou comme produit détachant (moquette, tapis, …). On se propose d'étudier la solution S d'ammoniac de concentration CS : S est 100 fois plus diluée que S0. Faire la liste de la verrerie nécessaire pour préparer précisément un volume V = 1,00 L de S à partir de S0. Le facteur de dilution étant de 100 et le volume de la fiole jaugée de 1,00 L, il faut utiliser une pipette jaugée de 1000 / 100 = 10,0 mL. Pisette d'eau distillée, pipeteur et bécher. Titrage de la solution diluée S : On se propose de vérifier la valeur de la concentration C0 de S0. Pour cela, la solution S est titrée par une solution d'acide chlorhydrique de concentration Ca = 0,015 mol.L-1. Dans un volume VS = 20 mL de la solution S, on verse progressivement la solution d'acide chlorhydrique et on mesure après chaque ajout le pH du mélange. On peut alors tracer la courbe d'évolution du pH en fonction du volume de solution acide ajoutée Va à l'aide d'un logiciel approprié. On trace aussi la courbe d'évolution de la dérivée dpH/dVa en fonction de Va.     Faire un schéma légendé du dispositif expérimental de titrage. Écrire l'équation bilan de la réaction de titrage (1) de la solution d'ammoniac S. NH3(aq) + H3O+(aq) =H2O( l) +NH4+(aq). H3O+(aq) / H2O( l) : pKa1 = 0 À partir des données expérimentales, déterminer le volume de solution acide versé à l'équivalence VaE. Préciser la méthode employée. La courbe dpH/dVa présente un pic à l'équivalence ; ou bien méthode des tangentes : En déduire la valeur de la concentration CS de la solution diluée S. A l'équivalence, les quantités de matière des réactifs mis en présence sont en proportions stoechiométriques : VS CS = VaE Ca soit CS = VaE Ca / VS = 14*0,015/20 =0,0105 ~ 0,11 mol/L. Déterminer alors la valeur de la concentration C0 de la solution S0. C0 = 100 CS = 1,1 mol/L, en accord avec la valeur de l'énoncé. Autre repérage de l'équivalence : Parmi les indicateurs colorés du tableau ci-dessous, déterminer celui qu'il faut ajouter à la solution pour procéder le plus efficacement possible au titrage précédent par une méthode colorimétrique. Justifier ce choix. Qu'observe-t-on autour de l'équivalence dans ce cas ? Indicateur coloré Teinte acide Zone de virage Teinte basique Bleu de bromophénol jaune 3,0 - 4,6 Bleu-violet Rouge de méthyle Rouge 4,2 - 6,2 Jaune Rouge de crésol Jaune 7,2 - 8,8 Rouge La zone de virage de l'indicateur coloré doit contenir le pH du point équivalent, c'est à dire environ 5,5. D'où le choix du rouge de méthyle. Avant l'équivalence la solution dans le becher est jaune ( NH3 en excès) ; après l'équivalence cette solution est rouge.     Web www.chimix.com Etude de l'équilibre dans la solution diluée S : On considère maintenant un volume US = 1,0 L de la solution S. Réaction acido-basique dans S : l'équation bilan, notée (2) de la réaction entre l'ammoniac et l'eau est : NH3(aq) + H2O(l ) = NH4+(aq) + HO-(aq) (2) Donner l'expression littérale de la constante d'équilibre K associée à l'équation de la réaction (2). K = [NH4+(aq)][ HO-(aq)] /[NH3(aq)] Exprimer K en fonction de Ke et Ka2. Calculer K. Or NH4+(aq) +H2O(l )= NH3(aq) + H3O+(aq) ; Ka2=[NH3(aq)][H3O+(aq)] / [NH4+(aq)] soit [NH4+(aq)] /[NH3(aq)] = [H3O+(aq)] / Ka2 . Repport dans l'expression de K : K =[ HO-(aq)] [H3O+(aq)] / Ka2 = Ke/Ka2 =10-14/10-9,2 = 10-4,8 = 1,6 10-5. Compléter le tableau d'avancement, ci-dessous, associé à la transformation modélisée par la réaction d'équation (2). Le volume étant US= 1L on peut confondre concentrations et quantités de matière. avancement (mol) NH3(aq) + H2O(l ) = NH4+(aq) + HO-(aq) début 0 CSUS solvant en large excès 0 0 en cours x CSUS-x xéq xéq équilibre xéq CSUS-xéq xéq xéq En supposant que xéq est négligeable par rapport au produit CS.US, montrer que : K~ xéq2 / (CSUS2). [NH4+(aq)] =[ HO-(aq)] = xéq/US ; [NH3(aq)] = (CSUS-xéq)/US~CS Repport dans K = [NH4+(aq)][ HO-(aq)] /[NH3(aq)] = xéq2 / (CSUS2). En déduire la valeur xéq. L'hypothèse est-elle justifiée ? xéq =[KCS]½ US =[1,6 10-5 *0,011]½ = 4,2 10-4 mol. 4,2 10-4 est très inférieur à 0,011 : l'hypothèse est donc justifiée. Etude conductimétrique : La valeur de la conductivité de la solution diluée S est s = 8,52.10-3 S.m-1. Valeurs des conductivités molaires ioniques (en S.m2.mol-1) : lHO- = 199.10-4 ; l NH4 + = 73,4.10-4. En déduire la valeur commune de la concentration (en mol.L-1) des ions NH4+(aq) et HO-(aq) dans la solution S. s = lHO-[ HO-(aq)] +l NH4 + [NH4+(aq)] = (lHO-+l NH4 +)[ HO-(aq)] [ HO-(aq)] = s / (lHO-+l NH4 +) = 8,52.10-3 /( 199.10-4 +73,4.10-4) [ HO-(aq)] =8,52 / (19,9+7,34) =0,313 mol m-3 = 3,13 10-4 mol/L. Déterminer alors la valeur du pH de la solution S. Ce résultat est-il en accord avec les données expérimentales ? [H3O+(aq)] = Ke / [ HO-(aq)] = 10-14 / 3,13 10-4 =3,19 10-11 mol/L pH= -log [H3O+(aq)] = -log 3,19 10-12 = 10,5, en accord avec la valeur expérimentale.

retour -menu