Particule chargée dans un champ électrique d'après IMRT En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

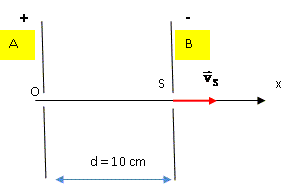
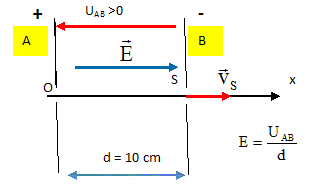
Un proton H+ pénètre entre deux électrodes A et B, planes, parallèles, soumises à une tension UAB, et séparées d'une distance d= 10 cm. Sa vitesse initiale peut être considérée comme nulle. Donner les caractéristiques du champ électrique E régnant entre les plaques. Donner la realtion entre la valeur E du champ, la tension UAB et la distance d. Préciser le signe de UAB . Le champ électrique pointe vers le plus petit potentiel, celui de B ; Le potentiel de A est supérieur à celui de B; UAB est positive. 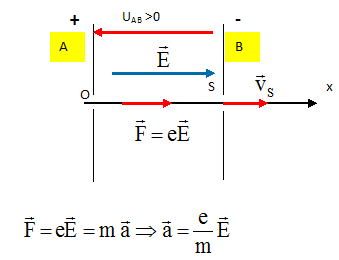Donner qualitativement ( sans démonstration), les caractéristiques du mouvement du proton entre les deux plaques. Trajectoire : droite OS ; la vitesse du proton augmente de O à S : le proton est accéléré. Le mouvement est rectiligne uniformément accéléré. La vitesse du proton, à la sortie des plaques, vaut VS =2000 km/s. En appliquant le théorème de l'énergie cinétique, déterminer la tension UAB. Le poids du proton est négligeable devant la force électrique F= eE. Le travail de la force électrique est moteur et vaut : eUAB. L'énergie cinétique initiale est nulle : ½mV2S = eUAB. Données : e = 1,6 10-19 C ; m = 1,66 10-27 kg ; VS = 2,0 106 m/s. UAB = 0,5*1,66 10-27 *(2 106)2 / 1,6 10-19 =20750 V ~ 21 kV. En déduire la valeur du champ E. E= UAB / d avec UAB = 20750 V et d= 0,1 m E = 20750/0,1 = 2,1 105 V m-1. En appliquant les lois de Newton, établir les équations horaires de la vitesse et de la position du proton entre les deux plaques. La seconde loi de Newton s'écrit, sur l'axe Ox : a = eE/m a = 1,6 10-19 *2,1 105 / 1,66 10-27=2,0 1013 m s-2. La vitesse est une primitive de l'accélération et la vitesse initiale est nulle : v = eE /m t. v = 2,0 1013 t. La position est une primitive de la vitesse : x =½eE/m t2. x = 1013 t2. En déduire la durée du parcours du proton entre les deux plaques. t2 = d / 1013 = 0,1 / 1013 = 10-14 ; t = 10-7 s. Calculer la vitesse de sortie VS à partir des équations horaires. VS = 2,0 1013 t = 2,0 1013 * 10-7 = 2,0 106 m s-1 = 2000 km s-1. Définir et calculer la vitesse moyenne du proton entre O et S. Vitesse moyenne = distance parcourue / durée = 0,1 / 10-7 = 1,0 106 m s-1 = 1000 km s-1. C'est à dire la moitié de VS.

retour -menu