Electron dans un champ électrique, spectrographe de masse d'après IMRT En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

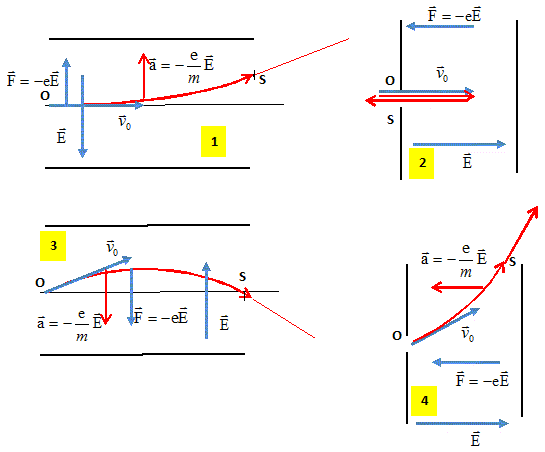
Trajectoire d'une particule dans un champ électrique : Un faisceau d'électron aborde une région dans laquelle règne un champ électrique supposé uniforme, crée par deux plaques parallèles reliées aux bornes d'un générateur. Représenter le champ électrique existant entre les plaques.   Les électrons sont soumis à une force électrique colinéaire au champ électrique mais de sens contraire ( la charge est négative). Le vecteur accélération est du même sens que la force, de sens contraire au champ électrique. Dans quel(s) cas peut-on affirmer que l'énergie de la particule est la même en S et en O. La force électrique est une force conservative ; le poids de l'électron est négligeable devant la force électrique. Dans les quatre cas l'énergie mécanique de l'électron se conserve entre O et S. Dans le cas de la figure 1, les électrons sont reçus en I sur un écran perpendiculaire à la direction OO'. L = 50 cm ; E = 100 V m-1 ; largeur des plaques l = 5,0 cm vitesse initiale en O : v0 = 2,0 106 m/s.   Parmi les propositions suivantes, donnant l'expression de Y, une seule est exacte. Laquelle ; justifier par une analyse dimensionnelle. 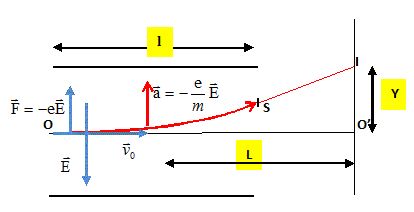1 2 3 4 5 eELl v02 eEl mv02 eELl m v02 eEl mv0 m eELl v02 Y a la dimension d'une longueur ; eE l a la dimension d'une énergie ; mv02 a la dimension d'une énergie ; 3 convient. Calculer la déviation O'I. On donne : m= 9,1 10-31 kg ; e = 1,6 10-19 C. eELl m v02 = 1,6 10-19 *100 *0,5*0,05 9,1 10-31 *4 1012 = 0,11 m Spectrographe de masse. Un proton de masse m et de charge q=e, placé dans un champ électrique uniforme E est soumis à une force électrique. Le champ électrique est obtenu en maintenant entre deux plaques conductrices parallèles et distantes de d= 10 cm une différence de potentiel U = 5,0 kV. Les plaques sont dans le vide et percées l'une en A et l'autre en D pour permettre le passage des particules. le proton est initialement au repos en A. Donner les caractéristiques de la force électrique F ; comparer sa valeur au poids du proton. La force électrique est colinéaire au champ électrique et a le sens du champ ( charge positive). E = U / d = 5000/0,1 = 5 104 V m-1 ; F = eE = 1,6 10-19 * 5 104 = 8,0 10-15 N. Poids du proton =P = mg = 1,67 10-27 *9,81 =1,6 10-26 N Le poids est négligeable devant la force électrique. Donner les caractéristiques de l'accélération du proton. La deuxième loi de Newton indique que l'acélération et la force électrique sont colinéaires et de même sens. eE m = 1,6 10-19 *5 104 1,67 10-27 = 4,8 1012 m s-2 Donner les caractéristiques du mouvement et de la trajectoire du proton entre A et D. L'accélération est constante : le mouvement est uniformément acéléré. La vitesse initiale est nulle : le mouvement est rectiligne suivant la direction du champ électrique. Calculer l'énergie cinétique puis la vitesse v du proton en D. Entre A et D seule la force électrique F = eE travaille ; son travail est moteur et vaut eU. Ecrire le théorème de l'énergie cinétique entre A et D : ½mv2-0 = eU = 1,6 10-19 * 5000 = 8 10-16 J. v =[ 2eU / m]½ =[ 2*8 10-16 / 1,67 10-27 ]½ =9,8 105 m/s. En D l'action du champ E cesse et le proton pénètre dans un champ magnétique uniforme B de valeur 0,08 T, perpendiculaire àla vitesse. 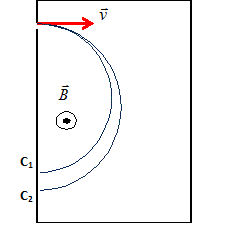Donner l'expression r de la circonférence de la trajectoire ; calculer r. r = mv eB = 1,67 10-27*9,8 105 1,6 10-19*0,08 = 0,128 m Comment évolue l'énergie cinétique du proton au cours du mouvement dans le champ magnétique ? Justifier. La force magnétique est perpendiculaire à la vitesse ; elle ne travaille pas. Le poids est négligeable devant la force magnétique ; le théorème de l'énergie cinétique indique que cette énergie est constante : la valeur de la vitesse reste constante. Une seconde particule de masse inconue M, de même charge q=e, également au repos en A, subit d'abord l'action du champ électrique , puis clle du champ magnétique dans les mêmes conditions. Le rayon de la trajectoire vaut R. Démontrer que : m M = r2 R2 Le champ électrique accélère les particules de charge e ; leurs vitesse finales sont telles que : ½mv2 = ½MV2 = eU ; mv2 = MV2. M m = v2 V2 (1) 2 Le champ magnétique dévie les particules sans modifier les valeurs des vitesses ; les rayons des trajectoires sont telles que : r = mv eB ; R = mV eB r R mv MV ou encore r2 R2 = m2 v2 M2 V2 tenir compte de (1) : m M = r2 R2 On mesure DC2 = 2R = 36,2 cm. Calculer M et identifier la particule. (r/R)2 =(12,8 /18,1)2 = 0,50 ; M = m / 0,50~ 2 m = 2*1,67 10-27 =3,34 10-27 kg ( deux fois la masse du proton ) La particule est un noyau de deutérium 21H.

retour -menu