Le Laser ; Iridium 192 en endocuriethérapie d'après DTS IMRT 1999 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

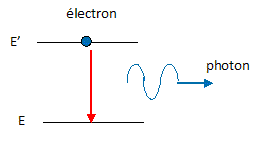
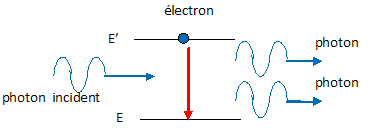
Expliquer en quelques lignes la signification des termes suivants : - émission spontanée ; - émission stimulée ; - pompage optique ; - inversion de population ; - faisceau directif Emission spontanée : un atome excité revient à un état de moindre énergie ( par exemple l'état fondamental) en émettant un photon. Celui-ci est émis dans une direction quelconque à une date quelconque. Emission stimulée : On peut aussi favoriser la désexcitation d’un électron en envoyant sur l’atome excité une lumière ( onde électromagnétique) dont la longueur d’onde correspondant à l’énergie de transition entre les deux états électroniques. On appelle ce phénomène l’émission stimulée (ou émission induite). Il y a amplification si les atomes sont plus nombreux à être dans l'état n' ( atome excité susceptible d'émettre) que dans l'état n (susceptible d'absorber) : il est nécessaire d'avoir une « inversion de population ». L’émission stimulée d’un atome ou d’une molécule donne un nouveau photon qui a exactement les mêmes fréquence, phase et direction que le photon incident ; dans un laser, cela se fait sur un très grand nombre d’atomes ou molécules identiques. Un laser émet une onde lumineuse intense dont la direction, la fréquence et la phase sont très bien déterminées. ( lumière cohérente).   Le faisceau laser diverge très peu, contrairement à celui d'une lampe torche : le faisceau laser est très directif. 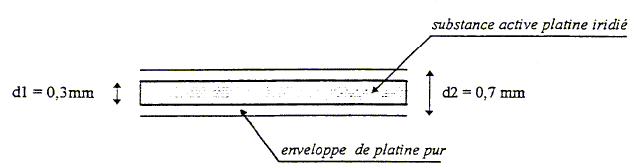Un laser Hélium-Néon de puissance 2 mW émet une lumière rouge de longueur d'onde l = 632,8 nm. Quelle différence d'énergie en eV y-a-t-il entre les deux niveaux ? D E = hc/l ; D E = 6,62 10-34 * 3 108 / 632,8 10-10 =3,14 10-18 J. Puis 3,14 10-18 /1,6 10-19 =19,6 eV. En déduire le nombre de photons émis par seconde. Energie délivrée en 1 s : puissance (W) * durée (s) = 10-3 J. Nombre de photons émis : 10-3 / 3,14 10-18 =3,18 1014 photons. Le faisceau laser a une divergence q= 1mrad. Quel est le diamètre de la tache observée sur un écran situé à 10 m de la source supposée ponctuelle ? q= 10-3 rad ; diamètre = 10 *10-3 = 0,01 m = 1 cm. L'iridium idium 19277Ir est un radio élément utilisé en endocuriethérapie. La source d'iridium 19277Ir est constituée d'un fil de platine iridié (alliage de platine et de 20 % d'iridium) formant la substance active, placé dans un tube de platine pur, servant d'enveloppe. Pour fabriquer cette source on irradie un fil de platine iridié ; au cours de cette irradiation neutronique, il se forme deux isotopes de l'Iridium selon les réactions : 19177Ir (n, g) 19277Ir et 19177Ir (n, g) 19477Ir Écrire les équations correspondant à l'actions des neutrons sur 19177Ir et formant les deux isotopes 192 et 194. 19177Ir +10n --->19277Ir* puis 19277Ir* ---> 19277Ir + g. 19177Ir + 310n --->19477Ir* puis 19477Ir* ---> 19477Ir + g. Les isotopes formés sont radioactifs : 19277Ir a une période T1 = 74 j ; 19477Ir a une période T2 = 19 h. Un échantillon de chaque isotope a une activité égale à 104 Bq, calculer dans chaque cas l'activité restante au bout de 8 jours. Montrer qu'il suffit d'un stockage de la source de 8 jours pour éliminer l'iridium 194. Loi de décroissance radioactive : A =A0 exp(-lt) avec l = ln2/T. l1 = ln2 / (74*24*3600) = 1,084 10-7 s-1 ; A = 104 exp(- 1,084 10-7 *8*24*3600)=9,28 103 Bq. l2 = ln2 / (19*3600) = 1,013 10-5 s-1 ; A = 104 exp(- 1,013 10-5 *8*24*3600)=9,1 Bq. L'activité de 19477Ir est égale au 1/1000 de sa valeur initiale au bout de 8 jours : il est pratiquement éliminé de la source. 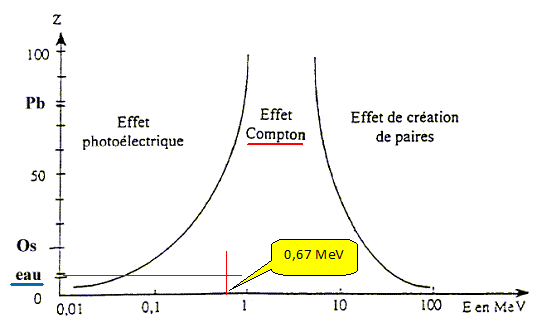Utilisation de l'Iridium 192 en endocuriethérapie. Dans un modèle simplifié, on considère que l'iridium 192 est radioactif ß-. L'énergie cinétique maximale des électrons émis est de 0,67 MeV. L'énergie des rayons g prend les valeurs suivantes ( en MeV) : 0,296 ; 0,308 ; 0,317 ; 0,468 ; 0,604 ; 0,612. Seuls les rayons g sont utilisés pour cette thérapie. Écrire l'équation de désintégration de l'iridium en précisant les lois de conservation utilisées. 19477Ir ---> AZX* +0-1e + antineutrino ; puis AZX* --> AZX +g Conservation de la charge : 77 = Z -1 d'où Z = 78 ( on identifie l'élément platine ) Conservation du nombre de nucléons : 194 =A+0. Expliquer le fait que dans la plupart des désintégrations l'électron est émis avec une énergie cinétique inférieure à 0,67 MeV. L'énergie est emportée par les photons gamma, les électrons et les antineutrino. L'énergie des photons est quantifiée ; le reste de l'énergie se répartit entre les électrons et les antineutrinos. Calculer la longueur d'onde du photon d'énergie 0,317 MeV. l = hc/E avec E = 0,317 106*1,6 10-19 =5,072 10-14 J. l = 6,62 10-34 * 3 108 / 5,072 10-14 =3,92 10-12 m. Justifier qualitativement l'existence des différents photons. L'énergie de l'atome est quantifiée : lors du retour de l'un des états excités vers un niveau de moindre énergie, il y a émission d'un photon. Étude de la source. Pour le traitement d'une tumeur, on utilise une source formée de 3 fils identiques de 8 mm de longueur, d'activité linéique (pour un diamètre donné) 7,4 ·107 Bq.cm-1 Calculer l'activité de la source en début de traitement. Longueur des trois fils : 0,8*3 = 2,4 cm ; A = 7,4 ·107 *2,4 =1,78 108 Bq. Que devient cette activité au bout de 5 jours de traitement ? l1 = ln2 / (74*24*3600) = 1,084 10-7 s-1 ; A = 1,78 108 exp(- 1,084 10-7 *5*24*3600)=1,70 108 Bq. Filtrage ou non des rayons ß- et g. Le faisceau d'électrons émis par la source d'énergie cinétique 0,67 MeV, traverse le tube de platine pur. Le transfert d'énergie linéique TLE est dans ce métal de 3,42 keV /µm. Quelle est la longueur de la trajectoire des électrons dans le platine ? Les caractéristiques du tube de platine sont-elles suffisantes pour assurer la protection du malade ? 0,67 MeV = 670 keV ; 670 / 3,42 =196 µm = 0,196 mm. Epaisseur du platine : ½(d2-d1) = 0,5(0,7-0,3) =0,2 mm, donc le malade est protégé des électrons.  La CDA (couche de demie atténuation) des rayons g d'énergie 0,317 MeV dans le platine pur est de 2,6 mm. Calculer le pourcentage de rayons g transmis au travers de l'enveloppe.  µ CDA = ln2 ; µ = ln2 / 2,6 = 0,267 mm-1. Epaiseur de l'enveloppe : 2 mm ; I = I0 exp(-µ x) =I0 exp(-0,267*0,2) =0,948 I0 (~ 95 % des rayons sont transmis). Quel est le type d'interaction prépondérant sachant que la tumeur soignée est de type tissus mous (constituée essentiellement d'eau) ? En donner une explication simple. Définir brièvement les trois effets qui apparaissent sur la figure. Effet photoélectrique : Lorsqu'un photon X, assez énergétique, arrive à proximité d'un électron d'une couche profonde, le photon est absorbé et un électron est éjecté : ce dernier emporte de l'énergie sous forme cinétique. La probabilité d'interaction par un effet photoélectrique est proportionnelle au cube du numéro atomique des atomes constituants le milieu. Un électron d'une couche superficielle vient prendre la place de l'électron éjecté : un photon de faible énergie (pour les atomes constitutifs des matières organiques) est émis. Effet Compton : Lorsqu'un photon X passe à proximité d'un électron périphérique peu lié à l'atome, l'énergie du photon est en partie transmise à l'électron : ce dernier est arraché de l'atome et s'échappe avec une certaine énergie cinétique. Le reste de l'énergie se retrouve sous la forme d'un photon X de direction différente et d'énergie inférieure. La probabilité d'interaction par un effet Compton ne dépend pas du numéro atomique. L'effet Compton est prépondérant dans les tissus organiques avec des photons X de grande énergie. Effet de matérialisation :  Le photon ( d' énergie supérieure à 1,02 MeV) disparaît : il donne naissance à un électron et à son anti-particule, le positon. Le coefficient d'atténuation massique pour l'eau est µ'=0,12 cm2 g-1 ; la masse volumique de l'eau r = 1 g cm-3. Calculer l'épaisseur traversée correspondant à l'absorption de 70 % du rayonnement. Loi de l'atténuation d'un faisceau monochromatique par un objet de densité uniforme : I = I0 exp (-µL) I0 : flux de rayons X incident ; I :flux de rayons X sortant ; µ : coefficient d'atténuation linéique du milieu ; L : épaisseur du milieu traversé. µ = µ'r =0,12*1 = 0,12 cm-1 ; I =0,3 I0. 0,3 = exp (-0,12 L) ; L = -ln(0,3) / (-0,12) = 10 cm.

retour -menu