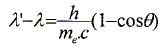Filtration des rayons X en radiodiagnostic d'après DTS IMRT 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Données : e = 1,602 10-19 C ; c = 3,00 108 m/s ; constante de Plank h= 6,626 10-34 J s. masse de l'électron : me = 9,11 10-31 kg = 0,511 MeV/c2 ; masse volumique du plomb rPb= 11,3 g cm-3 ; numéro atomique du tungstène Z(W) = 74. Niveaux d'énergie de l'atome de tungstène. Donner le nombre maximum d'électrons sur chacune des sous-couches s, p, d, f. s : 2 ; p : 6 ; d : 10 ; f : 14. En première approximation, les niveaux d'énergie d'un atome sont donnés par : E = -13,6 Z2/n2 ( eV) Calculer le niveau d'énergie E1 ( n=1) de l'atome de tungstène. E1 = -13,6 *742 = -74,5 keV. La valeur réelle est -69,5 keV. Comment expliquer cette différence ? La formule ci dessus ne prend pas en compte les interactions entre électrons. Elle permet simplement de trouver une valeur approximative de l'énergie. Emission de rayons X par le tungstène. On produit des rayons X dans un tube de Coolidge à anode de tungstène. Les électrons sont accélérés à l'aide d'une différence de potentiel U entre l'anode et la cathode de valeur 120 kV. On admettra les niveaux d'énergie suivants pour le tungstène : EK= -69,5 keV ; EL= -11,3 keV ; EM= -2,3 keV. Calculer l'énergie des photons provenant de l'émission des raies Ka et La ( en keV) Transition du niveau d'énergie zéro ( le plus haut ) au niveau K : 69,5 keV Transition du niveau M au niveau K : 69,5-2,3 = 67,2 keV Transition du niveau L au niveau K : 69,5-11,3 = 58,2 keV Transition du niveau d'énergie zéro ( le plus haut ) au niveau L : 11,3 keV Transition du niveau M au niveau L : 11,3-2,3 = 9,0 keV L'énergie des photons de la raie La varie t-elle si l'on abaisse la tension U à une valeur 30 kV ? Si oui, calculer la nouvelle valeur, sinon justifier. L'énergie de l'atome est quantifiée : le spectre de raies en énergie ne dépend que de la nature de l'atome considéré et en aucun cas de la haute tension appliquée entre anode et cathode : l'énergie des photons de la raie La ne varie donc pas. Le spectre des photons X obtenus résulte de l'addition d'un spectre continu et d'un spectre de raies. A quel phénomène est du l'existence du spectre continu ? Freinage des électrons par les atomes de la cible en tungstène. En bombardant un solide à l'aide un faisceau d'électrons, on observe un freinage et une déviation des électrons dûs champ électrique des noyaux de la cible. Or une charge électrique dont la vitesse varie rayonne d'après les équations de Maxwel. Le freinage des électrons n'est pas quantifiée : les énergies des photons ne sont pas quantifiées ; le spectre en énergie est continu. Quelle est l'énergie ( J et keV) des photons X les plus énergétiques que puisse émettre le tube ? La haute tension entre l'anode et la cathode détermine la forme du spectre continu de freinage et en particulier l'énergie maximale des rayons X émis. L'énergie maximale des photons X est égale à l'énergie cinétique finale Ec = eU des électrons arrivant sur la cible. Emax = 120 keV ; 120 103*1,6 10-19 = 1,92 10-14 J. 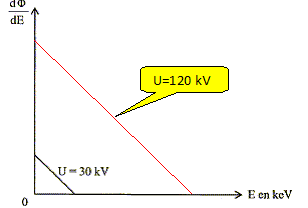L'évolution théorique du flux de rayonnement X en fonction de l'énergie est représentée ci-dessous pour une tension U= 30 kV.   Il s'agit d'une droite décroissante dont l'abscisse maximale et l'ordonnée maximale sont toutes deux proportionnelles à U. Représenter l'allure de l'évolution du flux du rayonnement X en fonction de l'énergie pour une tension U = 120 keV. 120 = 4 *30 ; abscisse maximale et ordonnée maximale sont multipliées par 4. Quels sont les effets sur le spectre des photons X de la traversée de la paroi du tube ? - absorption des photons de freinage de basse énergie. - si le verre contient du plomb, atténuation du faisceau. Atténuation des photons. 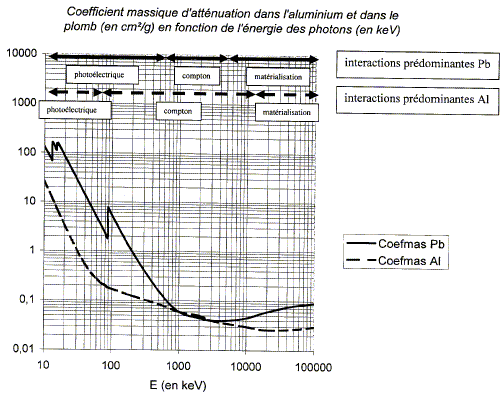L'énergie de liaison situé sur la couche K d'un atome de plomb est de 88 keV. Interactions des photons avec la matière. Définir et décrire l'effet photoélectrique. Lorsqu'un photon X, assez énergétique, arrive à proximité d'un électron d'une couche profonde, le photon est absorbé et un électron est éjecté : ce dernier emporte de l'énergie sous forme cinétique. La probabilité d'interaction par un effet photoélectrique est proportionnelle au cube du numéro atomique des atomes constituants le milieu. Un électron d'une couche superficielle vient prendre la place de l'électron éjecté : un photon de faible énergie (pour les atomes constitutifs des matières organiques) est émis. On envoie un photon d'énergie 100 keV sur du plomb. Quelle est l'énergie cinétique de l'électron émis par effet photoélectrique ? 100-88 = 12 keV. Un photon d'énergie E = 660 keV interagit par effet Compton avec un électron. Il projette cet électron en lui communiquant une énergie cinétique Ec= 97 keV, le reste étant emporté par un photon diffusé d'énergie E' faisant un angle q avec la direction du photon incident. Quelle relation existe t-il entre E, Ec et E' ? En déduire la valeur de E'. La conservation de l'énergie conduit à : E = Ec+E' ; E' = E-Ec = 660-97 = 563 keV. Calculer les longueurs d'onde l et l' des rayonnements incident et diffusé.  Convertir les énergies en joules : 660 103*1,6 10-19 = 1,056 10-13 J ; 563 103*1,6 10-19 = 9,0 10-14 J l = hc / E = 6,63 10-34*3 108 / 1,056 10-13 =1,88 10-12 m. l' = 6,63 10-34*3 108 / 9,0 10-14 =2,21 10-12 m. Déduire de la relation de Compton-Debye la valeur de q.   1 - cos q = (l' -l)mec / h = (2,21-1,88) 10-12 *9,1 10-31*3 108 / 6,63 10-34 = 0,136 cos q =1-0,136 =0,864 ; q = 30 °. Le choc n'est pas frontal ( dans ce cas on trouverait un angle de 180 °) Définir et décrire l'effet de matérialisation :  Le photon ( d' énergie supérieure à 1,022 MeV) disparaît : il donne naissance à un électron et à son anti-particule, le positon. Ces derniers s'anihilent immédiatement et donnent deux photons d'énergie 511 keV. Atténuation : énergie des photons et nature du milieu. Coordonnées de quelques points : energie ( keV) coefficient massique Pb ( cm2 g-1) coefficient massique Al ( cm2 g-1) 10 132,8 26,2 20 86 3,32 50 7,82 0,35 87,9 1,84 0,18 88,1 7,47 0,18 100 5,46 0,17 200 1,0 0,124 500 0,159 0,085 1000 0,06 0,06 5000 0,04 0,035 10 000 0,045 0,03 20 000 0,06 0,026 50 000 0,08 0,027 100 000 0,09 0,03 Atténuation provoquée par le plomb : Quel est la valeur du coefficient linéique d'atténuation du plomb pour un faisceau de photons de 20 keV ? de 200 keV ? masse volumique ( g cm-3) * coefficient d'atténuation massique ( cm2 g-1) 20 keV : m =11,3 *86 = 872 cm-1. 200 keV : m = 11,3 *1,0 = 11,3 cm-1. Un photon de 200 keV est-il plus pénétrant qu'un photon de 20 keV ? Justifier. m . CDA = ln 2. 20 keV : CDA = ln 2 / 872 = 8 10-4 cm 200 keV : CDA = ln 2 / 11,3 = 6 10-2 cm environ 100 fois plus grand que la valeur précédente (8 10-4 cm) Les photons d'énergie 200 keV sont plus pénétrants que ceux d'énergie 20 keV. Un photon de 100 MeV est-il plus pénétrant qu'un photon de 10 MeV ? Justifier. 10 MeV : m =11,3 *0,045 = 0,51 cm-1. 100 MeV : m = 11,3 *0,09 =1,0 cm-1. 10 MeV : CDA = ln 2 / 0,51 = 1,36 cm 100 MeV : CDA = ln 2 / 1,0 = 0,69 cm environ 2 fois plus petit que la valeur précédente (1,36 cm) Les photons d'énergie 10 MeV sont plus pénétrants que ceux d'énergie 100 MeV. 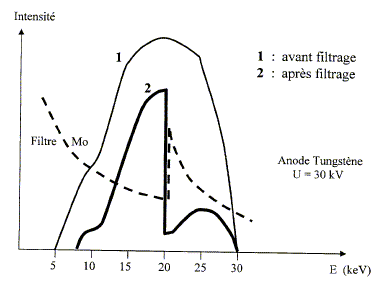Rôle du filtre : Interpréter la passage du spectre 1 au spectre 2. Une partie des rayons X sont absorbés par le filtre de molybdène ( en particulier, ceux de faible énergie). L'intensité des rayons X, après filtrage est égale à l'intensité des rayons X, avant filtrage, diminuée de celle des rayons absorbés par le filtre. On obtient la courbe 2 en retranchant aux valeurs de la courbe 1, les valeurs correspondantes de la courbe en pointillée ( flitre).

retour -menu