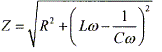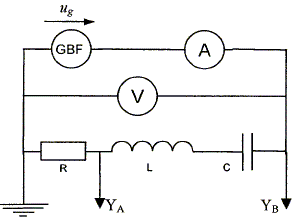
Circuit RLC série : d'après IMRT 06 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

On désire étudier le comportement d'un circuit RLC série. On dispose d'un générateur basse tension ( GBF), d'un oscilloscope, d'un ampèremètre (A) et d'un voltmètre ( V). R = 2000 ohms ; L = 1,00 H ; C = 1,00 microfarad. Le GBF doit produire une tension ug(t) = 15 cos (1000 pi t ) en volt. Quelle est la période de cette tension ? Pulsation w = 1000 pi rad/s ; Or w = = 2 pi /T ; T = 2 pi / w = 2 pi / (1000 pi) = 2,0 10-3 s. Quelle est son amplitude ? 15 V. Quelle sera la grandeur indiquée par le voltmètre ? Sur le voltmètre on lit la valeur efficace de la tension soit Ueff =Umax / 1,414 = 15/1,414 = 10,6 V. On rappelle que l'impédance d'un circuit RLC série s'exprime par : Calculer l'impédance Z du circuit. Lw = 1*1000*3,14 =3,14 103 ohms ; 1/(Cw) =1/(10-6*1000*3,14) =318,5 ohms (Lw -1/(Cw))2 = (3,14 103 +318,5)2 =1,196 107 R2 +(Lw -1/(Cw))2 = 4 106 + 1,196 107 =1,596 107 ; Z = 4,00 103 ohms. En déduire la valeur lue sur l'ampèremètre. Ieff = Ueff / Z = 10,6 / 4,00 103 = 2,65 10-3 A. 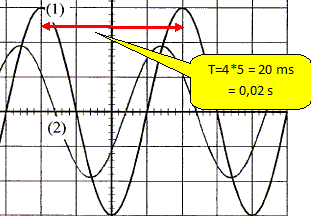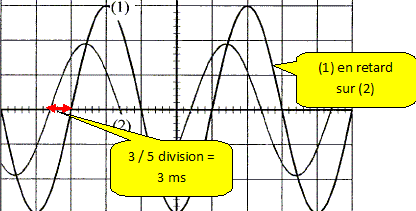On fait maintenant varier la fréquence du GBF. On obtient l'oscillogramme suivant : Voie A : (YA) 5 V / div ; Voie B : (YA) 5 V / div ; base de temps : 5 ms / div. Quelle est la fréquence de la tension appliquée au circuit ? f = 1/T = 1/0,02 = 50 Hz. Identifier la courbe correspondant à la voie A. Voie A : on visualise la tension aux bornes de la résistance uR(t) = Ri(t) Voie B : on visualise la tension aux bornes du dipole RLC ug(t) = Z i(t) Z > R donc l'amplitude de la tension ug(t) est supérieure à celle de la tension uR(t). YB : courbe 1. YA : courbe 2. La tension aux bornes du résistor R étant en phase avec l'intensité, déterminer le déphasage de la tension appliquée au dipole RLC par rapport à l'intensité du courant. Une période = 20 ms ou 2 pi radians déphasage de ug(t) sur i(t) : - 2 pi *3/20 = - 0,3 pi radian.   On étudie la résonance du circuit. On rappelle qu'à la résonance, l'impédance Z du circuit est minimum. Retrouver à partir de l'expression de Z, la relation qui permet de calculer la fréquence de résonance f0 en fonction des caractéristiques du circuit. Le terme (Lw0-1/(Cw0) est nu soit LCw02=1 avec w0 = 2 pi f0. Calculer f0. w02=1/ (LC) = 1/(10-6) ; w0 = 1000 rad/s ; f0. *= 1000/6,28 = 159 Hz. Quel est le déphasage entre la tension aux bornes du dipole RLC et l'intensité, à la résonance ? Tension aux bornes du dipole RLC et intensité sont en phase.

retour -menu