Cyclotron d'après DTS IMRT 04 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Le premier cyclotron 1,2 MeV construit se compose d'un électro-aimant dans l'entrefer duquel on loge une boîte métallique de diamètre 28 cm ( 11 pouces) maintenue sous vide. La chambre contient deux électrodes creuses en forme de "D" entre lesquelles est appliquées une tension alternative de 4000 V à haute fréquence. En son centre se trouve une source qui fournit des protons. Les protons décrivent une trajectoire dans le plan médian, du centre jusqu'au bord. Entre les dees, la seule force prépondérante est celle due à E. Dans les dees, la seule force prépondérante est celle due à B. 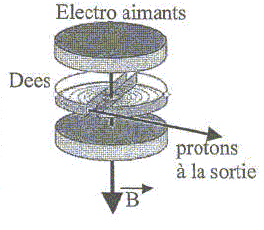Le cyclotron est constitué de deux "dees" D1 et D2 conducteurs, dans le vide desquels règne un champ magnétique uniforme constant B =1,8 T. On applique entre les dees une tension alternative sinusoîdale u(t) = Umax cos(wt) qui accélère les protons quand ils passent entre les dees. Les protons 11H sortent d'une chambre d'ionisation au voisinage du centre O de l'appareil avec une vitesse supposée négligeable au moment où la tension appliquée entre les dees est maximale Umax. On représenté la trajectoire de l'ion dans le cyclotron. Au point A2, repésenter le vecteur vitesse v de l'ion, la force magnétique Fm et en déduire le sens du champ magnétique B. 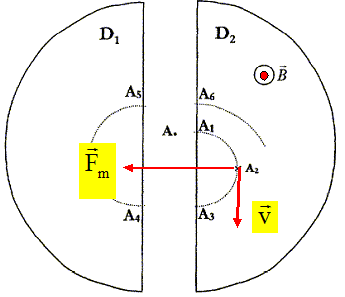Montrer que le champ magnétique ne modifie pas la valeur de la vitesse. La force magnétique est perpendiculaire à chaque instant à la vitesse : cette force ne travaille pas. Le poids du proton est négligeable devant la force magnétique. Donc l'énergie cinétique du proton ne varie pas et la valeur de la vitesse reste constante. 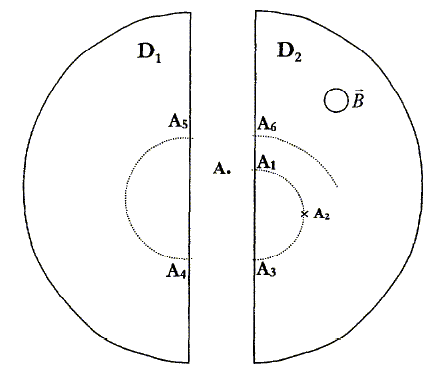Le mouvement du proton est ciculaire de rayon : r = mv eB Exprimer et calculer la durée t½ de passage de l'ion dans un "dee". Conclure. Les protons parcourent une demi circonférence de rayon r à la vitesse v de valeur constante : p r = v t½ avec r = mv/(eB) soit r/v = m/(eB) t½ = p r v = p m eB t½ : valeur constante, indépendante de la vitesse. 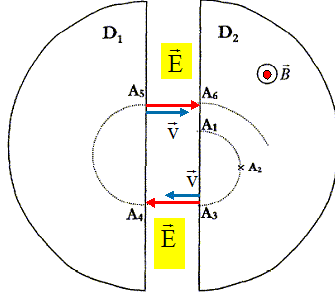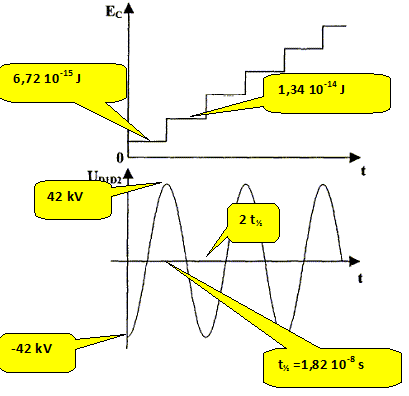t½ = 3,14*1,67 10-27 /(1,6 10-19*1,8) =1,82 10-8 s. Représenter le vecteur champ électrique dans les espaces A3A4 et A5A6 afin que le proton soit accéléré. La force électrique F= eE et le champ électrique sont colinéaires et de même sens, la charge étant positive. Il y a accélération si la force et la vitesse initiale sont colinéaires et de même sens. Quelle doit être la période T de la tension sinusoiale accélératrice ainsi que sa fréquence f ? Pour une accélération maximale, à chaque demi tour, la tension alternative doit changer de signe et prendre sa valeur maximale. La demi période de la tension alternative est égale à la durée d'un demi tour. T = 2t½ = 2p m / (eB) = 2*1,82 10-8 =3,64 10-8 s ; f = 1/T = 2,75 107 Hz.   Quelle est ( eV et J) la variation d'énergie cinétique DE des protons quand ils passent d'un "dee' à l'autre. Donnée : Umax =42 kV DE = eUmax = 42 keV = 42 000 *1,6 10-19 J =6,72 10-15 J. Quelle est ( eV et J) l'augmentation de leur énergie cinétique à chaque tour. 2*6,72 10-15 = 1,34 10-14 J. Compléter les courbes suivantes ( énergie cinétique totale aquise au cours du temps et tension UD1D2 )   Certians cyclotron posèdent 4 dees permettant d'accélérer 4 fois par tour les particules introduites. Quelle est alors l'énergie aquise par les protons en un tour, pour la même tension accélératrice ? L'énergie cinétique augmente de la valeur 6,72 10-15 J à chaque passage entre les dees. En un tour , ils passent 4 fois entre les dees, d'où : 4*6,72 10-15 = 2,69 10-14 J. Les protons effectuent 200 tours. Quelle est l'énergie cinétique de sortie ? 2,688 10-14 *200 =5,38 10-12 J.

retour -menu