Tomographie par émission de positons ( TEP) ; la mamographie: d'après DTS IMRT 01 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

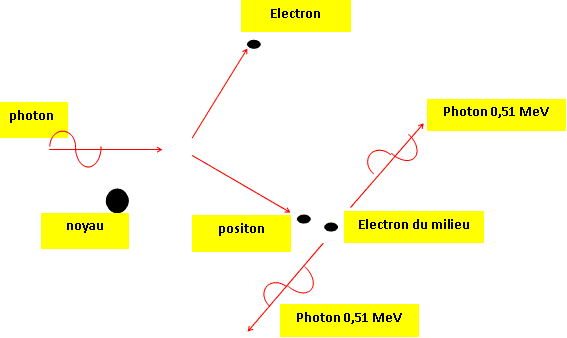
La TEP est fondée sur l'existence de radioéléments qui se désintègrent avec émission de positons. Lorsque cette émission se produit dans un milieu matériel, le positon se combine avec un électron du milieu et disparaît après un parcours très bref (1 à 3 mm). On obtient alors des photons g. La détection de deux photons émis en coïncidence permet de localiser le point d'annihilation. Ce dernier étant pratiquement confondu avec le point d'émission du positon, on dresse ainsi la cartographie du radioélément dans l'organe vivant étudié ». d'après « Le progrès technique 4-92 » Données : unité de masse atomique 1 u = 931,5 MeV.c-2 ; charge élémentaire e = 1,60 ·10-19 C, masse de l'électron me = 9,1 ·10-31kg célérité de la lumière c = 3,00 ·108 m.s-1 ; 1 MeV = 1,6 ·10-13 J Donner la masse et la charge du positon. Charge positive e = charge élémentaire e = 1,60 ·10-19 C ; masse du positon = masse de l'électron me = 9,1 ·10-31kg. Expliquer ce qui se passe entre l'émission du positon et la rencontre avec l'électron. Décrire l'interaction entre un positon et un électron. Le chemin suivi par le positon est très court, il est freiné par la matière et s'annihile en fin de course avec un électron du milieu. 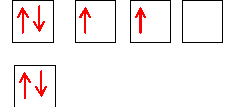Les éléments émetteurs de positons utilisés sont généralement des isotopes d'éléments constitutifs des organes comme l'oxygène ou le carbone. Ils remplacent l'élément stable car ils ont le même cortège électronique. En utilisant les quatre nombres quantiques, décrire le cortège électronique dans l'état fondamental du carbone qui possède 6 électrons. Représenter les cases quantiques. Indiquer sa position dans la classification périodique. 1 s2 2s2 2p2 ; deuxième période ; colonne 14. L'oxygène présente un isotope émetteur de positons noté 158O. Que représentent les nombres 8 et 15 ? Indiquer l'équation de la désintégration et énoncer les lois de conservation. Préciser le mécanisme de cette désintégration. Nombre de charge, nombre de proton, numéro atomique : Z=8 Nombre de masse, nombre de nucléons A=15. 158O ---> AZX + 01e. Conservation de la charge : 8 = Z+1 d'où Z = 7 ( élément azote) Conservation du nombre de nucléons : 15 = A+0. bêta + : le positon émis réagit immédiatement avec un électron du milieu (annihilation ) ; il en résulte la production de deux rayons gamma de 511 keV. Ces émetteurs de positons ont une « demi-vie » brève (de quelques minutes à quelques heures). Définir la demi-vie d'un radioélément. Durée au bout de laquelle l'activité initiale est divisée par deux. 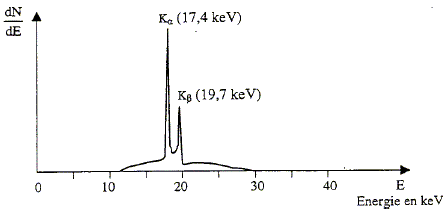La mamographie : constante de Planck h = 6,626 ·10-34 J.s ; 1 eV = 1,602 ·10-19 J charge élémentaire : e = 1,602 ·10-19 C ; 1 u = 931,5 MeV / c2 célérité de la lumière dans le vide : c = 3,0 ·108 m.s-1 ; masse de l'électron me = 9,1 ·10-31 kg = 5,5 ·10-4 u. Pour cet examen, on utilise des rayons X peu énergétiques et avec un spectre à bande étroite. 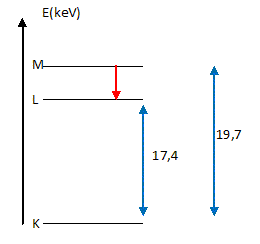On utilise souvent un appareil à anode de molybdène dont le spectre est le suivant : A quels phénomènes correspondent les pics Ka et Kb ? Tansitions électroniques : L ou K : nom de la couche d'arrivée des électrons au cours du réarrangement. Ka : l'électron provient de la couche immédiatement supérieure. un électron du niveau L passe au niveau K où une place a été libéré par l'arrachement d'un électron. Kb : l'électron provient d'une couche plus lointaine. un électron du niveau M ( par exemple) passe au niveau K où une place a été libéré par l'arrachement d'un électron. Si on attribue conventionnellement le niveau d'énergie 0 au niveau K de l'atome de molybdène, donner les énergies des niveaux L et M et les placer sur un diagramme où 5 keV sont représentés par 1 cm. Lorsqu'un atome de molybdène excité voit un électron de sa couche M revenir sur la couche L, il émet un photon. Indiquer cette transition sur le diagramme de la question précédente. Donner l'énergie du photon, calculer sa longueur d'onde dans le vide. Quelle est la nature de ce photon ? Energie du photon : E = 19,7-17,4 = 2,3 103 eV ou 2,3 103 *1,6 10-19 =3,68 10-16 J. Longueur d'onde dans le vide : l = h c / E =6,626 ·10-34*3 108 / 3,68 10-16 =5,4 10-10 m. Les RX sont un rayonnement électromagnétique de courte longueur d'onde (10-12 m à 10-8 m) Radiodiagnostic classique. Dans un tube utilisé pour ce genre de diagnostic, des électrons sont émis d'une cathode chaude avec une vitesse considérée comme nulle. Ils sont accélérés entre cette cathode et l'anode par une tension UAK = Vanode-Vcathode comprise entre 60 kV et 120 kV. Pour un examen on utilise une tension UAK = 80 kV. Donner l'expression de l'énergie cinétique des électrons arrivant sur l'anode si on néglige le poids de ces électrons devant la(es) autre(s) action(s). Faire l'application numérique et donner le résultat en keV puis en Joule. Ec = eUAK =1,6 *80 = 128 keV ou 128 103 *1,6 10-19 =1,28 10-14 J. Un courant de 40 mA traverse alors le tube. Calculer le nombre d'électrons arrivant sur l'anode en 0,1 s, durée d'une radiographie. Quelle est l'énergie cédée par l'ensemble de ces électrons lorsqu'ils sont arrêtés par l'anode ? Le résultat sera donné dans le système international. Q = I t avec I = 0,04 A et t = 0,1 s : Q = 0,04*0,1 = 4 10-3 C. Puis diviser par la charge élémentaire : n = 4 10-3 /1,6 10-19 =2,5 1016 électrons. Energie de ces électrons : 1,28 10-14 * 2,5 1016 =320 J. Calculer la puissance électrique du tube. Puissance (watt) = énergie (J) / durée (s) = 320/0,1 = 3200 W = 3,2 kW. (autre méthode : 0,04*80 103) Pour une tension UAK = 80 kV le rendement de ce tube est h = 0,8 %. Quelle est la puissance du faisceau de rayons X ? Quelle energie fournit-il pour une radiographie qui dure 0,1 s ? Puissance du faisceau : 3200*0,8/100 = 25,6 W. Energie fournie : 25,6*0,1 =2,56 J. Une grande partie de l'énergie consommée par le tube n'est pas restituée sous forme de rayons X ; sous quelle forme cette énergie apparaît-elle ? Sous forme de chaleur, l'anode chauffe. Quelle énergie est ainsi dissipée pour une radiographie qui dure 0,1 s ? 99,2 % de l'énergie du faisceau est dissipée en chaleur : 0,992*320 =317,4 J. Quelle élévation de température subit l'anticathode qui peut être considérée comme un bloc de cuivre de masse 500 g et de capacité thermique massique (ou chaleur massique) Cc = 150 J.kg-1.K-1 ? Energie (J) = masse ( kg) * chaleur massique * élévation de température Q = m Cc Dq ; Dq = Q / (m Cc) =317,4 /(0,5*150)= 4,2 °C. Utilisation des rayons X de très haute énergie. L’appareil MINAC permet de radiographier des pièces métalliques en utilisant des rayons X produits à partir d’électrons accélérés (énergie cinétique de 4 MeV). Dans ces conditions, la profondeur de pénétration maximale des rayons X est d’environ 40 cm. Rappeler la loi d’absorption des photons par la matière en précisant la signification de chaque lettre de l’expression. Loi de l'atténuation d'un faisceau monochromatique par un objet de densité uniforme : I = I0 exp (-µL) I0 : flux de rayons X incident ; I : flux de rayons X sortant ; µ : coefficient d'atténuation linéique du milieu ; L : épaisseur du milieu traversé. On admet qu’à 40 cm dans l’acier, 99 % des photons ont été absorbés. Calculer le coefficient linéique d’absorption totale de ces photons dans l’acier (dans le système international), puis la valeur de la couche de demi-atténuation. L = 0,4 m ; I = (1-0,99) I0 = 0,01 I0 ; µ L = ln(I0/ I) = ln(1/0,01) =4,605 ; µ = 4,605/L = 4,605 / 0,4 =11,5 m-1. Couche de demi-absorption : ½I0 = I0 exp (-µ . CDA) ; µ . CDA = ln 2. CDA(acier) = ln 2 / 11,5 =0,060 m = 6,0 cm.

retour -menu