circuit RLC : QCM d'après DTS IMRT 01 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

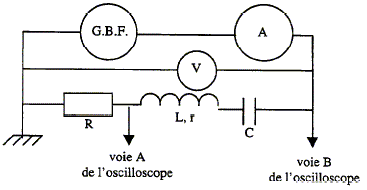
Répondre par vrai ou faux. Justifier ( une seule bonne réponse) R= 20 ohms ; bobine : L = 0,5 H et r = 10 ohms ; C = 10 microfarads. La fréquence du GBF est réglable ; le GBF délivre une tension alternative sinusoïdale de fréquence N Le voltmètre permet de connaître : A- la valeur maximale de la tension. Faux L'oscilloscope permet de connaître la valeur maximale de la tension. B- la valeur efficace de la tension. Vrai C- la valeur instantanée de la tension. Faux. L'oscilloscope permet de visualiser les valeurs instantanées de la tension. La valeur instantanée de l'intensité est connue à partir de : A- la voie A de l'oscilloscope. Vrai On visualise la tension aux bornes du conducteur ohmique R : la tension aux bornes de ce dernier et l'intensité qui le traverse sont proportionnelles. B- la voie B de l'oscilloscope. Faux. On visualise la tension aux bornes du dipole RLC C- l'ampèremètre. Faux. L'ampermètre donne la valeur de l'intensité efficace. L'impédance Z du dipôle : A- est indépendante de la fréquence N de la tension alternative. Faux. B- augmente avec cette fréquence. Faux. C- varie avec cette fréquence. Vrai. Z = [(R+r)2 + (Lw-1/(Cw)2]½ avec w = 2 pi N. Lorsque la fréquence N = 100 Hz, l'impédance vaut : A-158 ohms. Vrai. w = 2 pi N = 2*3,14*100 = 628 rad/s : L w = 0,5*628 = 314 ohms ; 1 /(C w) = 1/(10-5*628) = 159 ohms. L w - 1 /(C w) =155 ohms ; R+r = 30 ohms ; Z = [(R+r)2 + (Lw-1/(Cw)2]½= Z = [302 + 1552]½ =158 ohms B- 30 ohms. Faux. C- 273 ohms. Faux. L'impédance peut aussi être mesurée par : A-Ueff / Ieff. Vrai. B- Ieff /Ueff. Faux. C- u(t) / i(t). Faux. Le régime imposé est celui : A- d'oscillations libres amorties. Faux. Le GBF impose sa fréquence au dipôle RLC. B- d'oscillations libres entretenues. Faux. C- d'oscillations forcées. Vrai. La résonance d'intensité se manifeste quand : A- u(t) et i(t) sont en phase. Vrai. B- les tensions instantanées aux bornes de la bobine et du condensateur ont la même valeur. Faux Ces deux tensions sont en opposition de phase et ont la même valeur efficace. C- la tension aux bornes de la bobine et l'intensité sont en phase. Faux La résonance a lieu pour une fréquence de. A- 204 Hz. Faux LCw02 = 1 ; w02 = 1/(LC) = 1/(0,5 10-5) =2 105 ; w0 =447,2 rad/s. N0 = w0 /( 2 pi ) = 447,2 / 6,28 = 71,2 Hz. B- 113 Hz. Faux C- 71,2 Hz. Vrai La puissance moyenne consommée par ce dipôle est P = Ueff Ieff cos j ( j déphasage entre u(t) et i(t). A la résonance : A- P = Ueff Ieff . Vrai u(t) et i(t) sont en phase ; cos j = cos 0 = 1. B- P = Umax Imax . Faux C- P = u(t) i(t). Faux Il s'agit de la puissance instantanée. La puissance consommée l'est essentiellement : A-par effe t Joule. Vrai B- par l'apparition du champ magnétique dans la bobine. Faux  C- par l'apparition du champ électrique dans le condensateur. Faux.

retour -menu