Dipôle (RLC), étude énergétique, concours manipulateur radio Poitiers 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

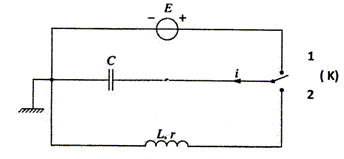
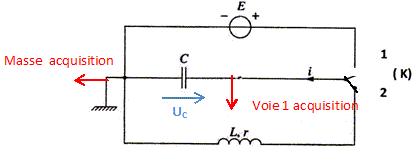
On réalise le montage suivant avec un générateur de fem E. Le condensateur a une capacité C = 0,50 µF. A l'instant de date t = 0 s, on ferme l'interrupteur K en position 2 et on enregistre, grâce à un dispositif d'acquisition, les variations de la tension aux bornes du condensateur. Indiquer sur la figure le branchement à faire vers la carte d'acquisition pour obtenir la tension aux bornes du condensateur ; y figurer également la tension aux bornes du condensateur. 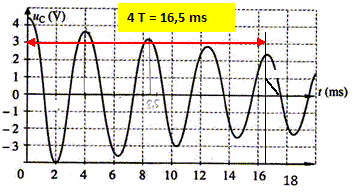La décharge du condensateur est représentée sur la figure suivante : Déterminer la pseudo-période T des oscillations. T = 16,5/4 =4,13 ms ~ 4,1 10-3 s. Donner l'expression de la pseudo-période assimilée à la période propre d'une oscillation périodique. T= 2 pi ( LC)½. Faire une analyse dimensionnelle de T. pi est sans dimension ; Emagn = ½ Li2 soit L = 2 Emagn / i2 ; L est une énergie divisée par une intensité au carré. L : J A-2. Eélec = ½ q2 /C soit C = ½ q2 /Eélec; C est une une charge au carré divisée par une énergie de plus une charge est une intensité fois un temps d'où : C : J-1 A2s2 Par suite (LC)½ a la dimension d'un temps. En déduire la valeur de l'inductance L. T = 4,13 10-3 s ; L = T2 / (4pi2 C) =[ 4,13 10-3 ]2 /(4*3,142*5 10-7) =0,864 ~0,86 H. Exprimer , puis calculer l'énergie stockée dans le condensateur à la date t = 4 ms. Quelle est l'énergie stockée dans le circuit à la même date ? Justifier. A cette date, le graphe indique que la tension aux bornes du condensateur passe par une valeur maximale, voisine de UC = 3,6 V ; [dUC / dt ] t = 4 ms =0 ; [dq / dt ] t = 4 ms =0 ; or i = dq / dt donc i(t=4 ms) =0 ; la bobine ne stocke pas d'énergie à cette date ; le condensateur stocke donc toute l'énergie du dipôle RLC.  E = ½CUC2 =0,5*5 10-7*3,62 =3,24 10-6 J ~3,2 10-6 J.   Calculer l'intensité du courant circulant un quart de période après la date t = 4 ms. On négligera l'amortissement entre les dates t et t+T/4. UC ( t+T/4) = 0 d'après le graphe ; le condensateur ne stocke pas d'énergie ; la bobine stocke toute l'énergie du dipôle RLC. En négligeant l'amortissement : 3,24 10-6 = 0,5 L i2 ; i = [2* 3,24 10-6 / L]½ = [2* 3,24 10-6 / 0,864]½ =2,74 10-3~2,7 10-3 A. Quel est l'origine de l'amortisement ? Au cours des échanges d'énergie entre bobine et condensateur, une partie de l'énergie est dissipée sous forme de chaleur ( effet Joule) dans les parties résistives du circuit ( résistances des fils et de la bobine).

c

retour -menu