Condensateur et bobine ( concours manipulateur radio Tours 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

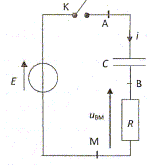
Générateur, conducteur ohmique et condensateur. Le condensateur a été déchargé et on réalise le montage : A l'instant de date t = 0, on ferme I'interrupteur K. $oit i I'intensite du courant et q la charge du condensateur. La tension UAB aux bornes du condensateur sera notee uc. Exprimer q en fonction de uc. q = C uc. Exprimer UBM en fonction de i, puis de q, puis de uc. UBM = R i avec i = dq/dt = Cduc/dt ; UBM = RCduc/dt. Etablir I'équation differentielle satisfaite par Uc pour t positif ou nul. Additivité des tensions : uc+UBM = E ; uc+RCduc/dt = E duc/dt + uc/(RC) = E/(RC). (1) Que vaut uc(0) ? Justifier. A l'instant initial t=0, le condensateur est déchargé q (0) = 0. q(0) = C uc(0) conduit à uc(0) = 0, la capacité C n'étant pas nulle. Vérifier que uc =E(1-exp(-t/to)) est solution de I'équation différentielle pour une valeur particuliere de to dont on donnera l'expression. duc /dt = E/ to exp(-t/to)), repport dans (1) E/ to exp(-t/to)) + E/(RC)(1-exp(-t/to)) = E/(RC) [E/ to -E/(RC) ]exp(-t/to)) + E/(RC) = E/(RC) Cette égalité est vérifiée quel que soit le temps si to = RC. Quelle est la valeur prise par Uc lorsque t tend vers l'infini ? Justifier. exp(-t/to)) tend vers exp(-oo) = 0 ; (1-exp(-t/to)) tend vers 1 ; uc tend vers E. Calculer I'energie alors emmagasinee dans Ie condensateur. Données: E = 5,0 V et C= 2,0 µF. Eél = ½Cu2c = ½CE2 = 0,5*2,0 10-6 * 52 = 25 10-6 = 2,5 10-5 J. 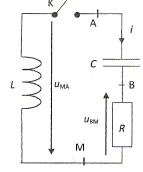Bobine, d'inductance L, est considérée comme idéale. 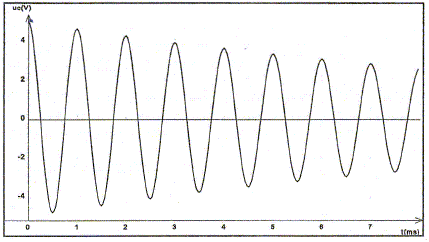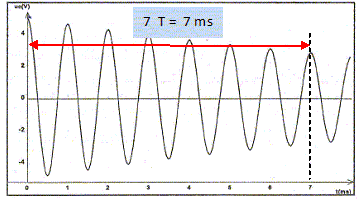A I'instant de date t = 0, on ferme Ie circuit : Le condensateur a été préalablement chargé, de sorte que uc(0) = 5,0 V. L'évolution de la tension uc au cours du temps est obtenue avec un dispositif d'acquisition de données relié à un ordinateur. Donner I'expression de UBM en fonction de i, puis.de q, puis de uc. UBM = R i avec i = dq/dt = Cduc/dt ; UBM = Rdq/dt = RCduc/dt . Donner I'expression de UMA en fonction de i, puis de q, puis de uc. UMA = Ldi/dt avec di/dt = d2q/dt2 = Cd2uc/dt2. UMA = Ld2q/dt2 = LCd2uc/dt2. Déduire l'équation différentielle satisfaite par uc. Additivité des tensions : uc + UMA + UBM=0 uc + LCd2uc/dt2 + RCduc/dt = 0 d2uc/dt2 + R/Lduc/dt + uc /(LC) = 0.  Comment nomme-t-on Ie régime d'oscillations obtenu ? Oscillations libres périodiques amorties ( pseudopériodique). Mesurer un temps caractéristique des oscillations à partir du document.   Une pseudopériode est égale à 1 ms = 10-3 s. En déduire la valeur de I'inductance L de la bobine. On donne pi2 ~ 10 ; 1/80~0,012. T = 2 pi (LC)½ ; L = T2 /(4 pi2C) = 10-6 / (4*10* 2,0 10-6) =1/80=0,012 =12 mH.

retour -menu