QCM, scintigraphie, boule de pétanque et cochonnet ( concours manipulateur radio AP HP 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Un condensateur de capacité C = 10,0 nF est chargé sous une tension de 5,00 V. L'énergie emmagasinée est : A B C( vrai) D 2,5 10-7 J 250 nJ 125 nJ 125 µJ Analyse : E = 0,5 CU2 = 0,5*10-8 *52 =12,5 10-8 J = 125 10-9 J = 125 nJ.  Un condensateur est chargé par un courant continu d'intensité I= 2,0 mA pendant 1 minute. Sa charge q est alors de : A B( vrai) C D 120 C 0,12 C 0,002 C 2 µC Analyse : Charge à intensité constante Q = I t = 2,0 10-3 * 60 =0,12 C .  Un dipole RC comportant une résistance R = 10 kiloohms et un condensateur de capacité C = 30 nF a pour constante de temps : A (vrai) B C D 0,30 ms 0,30 s 3 10-12 s 3,0 s Analyse : RC = 104 * 30 10-9 = 3,0 10-4 s = 0,30 ms. Scintigraphie thyroïdienne. Pour étudier Ie fonctionnement de la glande thyroïde,on réalise une scintigraphie thyroïdienne en injectant au patient de l'iode 123 (12353I). Donner la composition du noyau d'iode 123. le noyau d'iode 123 compte : 53 protons ; 123 -53 = 70 neutrons. Pour réaliser cette scintigraphie, on doit injecter au patient de l'iode 123 prélevé dans un flacon en verre stocké dans un pot en plomb. Trois heures plus tard, son activite mesurée est de 170 MBq, l'activité initiale de l'iode 123 étant de 199 MBq. Définir Ie temps de demi-vie d'un élément radioactif. Durée au bout de laquelle l'activité initiale est divisée par deux. On rappelle que la loi de décroissance radioactive s'écrit A(t) = A0 exp(-lt) où A(t) représente l'activité d'un échantillon à la date t et A0 son activité à la date t =0. Déterminer en h-1 la valeur de la constante radioactive. -lt = ln(A/A0) ; l = 1/t ln(A0/A) = 1/3 ln(199/170)=5,25 10-2 h-1~ 5 10-2 h-1. En déduire Ie temps de demi-vie. t½ = ln 2 / l =ln2 / 5,25 10-2 =13,2 h ~ 13 h. L'acquisition des images se fait 4 heures après l'injection au patient de quelques millilitres de solution contenant l'iode 123 d'activité mesurée au moment de l'injection de 5 MBq. Calculer son activité au bout de 4 heures. A(t) = A0 exp(-lt) = 5 exp(-5,25 10-2*4) =4,05 MBq~ 4 MBq. Dans Ie cadre d'un traitement d'une hyperthyroïdie ou d'un cancer thyroidien, on utilise de l'iode 131 (13153I). Comment nomme-t-on les noyaux (12353I) et 13153I ? Justifier votre réponse. Isotopes : même numéro atomique et des nombres de neutrons différents. Le noyau d'iode 131 est émetteur ß-. 21Sb ; 52Te ; 53I ; 54Xe ; 55Cs m(13153I)= 130,87697 u ; 1 eV = 1,60 10-19 J ; m(Xe)=130,87538 u ; c = 3,00 108 m/s ; m(e)= 0,00055 u ; 1u = 1,66054 10-27 kg. Après avoir précisé les lois de conservation utilisées, écrire l'équation de sa désintégration. 13153I ---> AZX + 0-1e conservation de la charge : 53 = -1 + Z d'où Z =54 ( élément Xénon) conservation du nombre de nucléons : 131 = 10 + A d'où A=131 Donner l' expression littérale de l'énergie libérée lors de la désintégration d'un noyau d'iode 131. La calculer en joule puis en MeV. perte de masse : Dm = m(Xe) + m(e) - m(13153I). Dm =130,87538 +0,00055-130,87697 = -0,00104 u =-0,00104*1,66054 10-27 kg=-1,72696 10-30 kg E = Dm c2 = -1,72696 10-30*(3,00 108)2 = - 1,55 10-13 J - 1,55 10-13 / 1,60 10-19 = -9,71 105 eV =-0,971 MeV. Pour ce traitement, Ie patient ingère une gelule contenant 1,00 µg d'iode 131. Calculer la masse résiduelle d'iode 131 au bout d'une durée égale à 10 demi-vies. m(t) = m0 exp(-lt) avec l = ln2 / t½ et t = 10 t½ ; lt =10 ln 2 m(t) = 1,00 exp(-10ln2) = 9,77 10-4 µg. 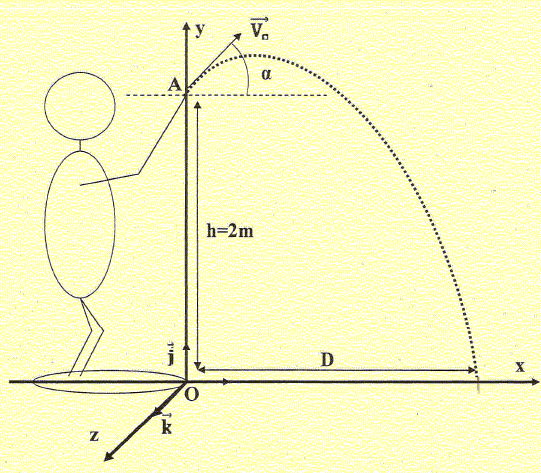La boule de pétanque et le cochonnet. La pétanque est pratiquée dans Ie sud de la France. Le but du jeu est d'approcher la boule en acier, de masse 700 g, Ie plus près possible du cochonnet, boule en buis de masse 15 g. Pour commencer une partie, il faut que Ie cochonnet soit entre 6 et 10 m du cercle où se trouve le tireur. On étudie Ie mouvement du cochonnet et de la boule de pétanque dans le repère orthonormé (0 ; i ; j ; k). L'origine O du repère est le point du sol situé à la verticale du centre d'inertie du cochonnet placé initialement en A. Le cochonnet est lancé à la date t = 0 s avec une vitesse v0: faisant un angle a=45° avec 1'horizontale. g = 10 N/kg   Quelles sont, sous forme littérale, à la date t = 0 s dans le repère donné les coordonnées du vecteur position OA et du vecteur vitesse v0 ? Un vecteur est écrit en gras et en bleu. OA = 0 i + h j + 0 k. v0 = v0 cos a i + v0 sin a j + 0 k. Etablir dans le repère, sous forme littérale, les coordonnées du vecteur accélération, du vecteur vitesse, et du vecteur position du centre d'inertie G du cochonnet. Le mouvement est une chute libre ( la seule force est le poids du cochonnet) a = 0 i -g j + 0 k. Le vecteur vitesse est une primitive du vecteur accélération : v= v0 cos a i +(-gt + v0 sin a) j + 0 k. Le vecteurposition est une primitive du vecteur vitesse : OM= v0 cos a t i +(-½gt2 + v0 sin at + h) j + 0 k. Déduire sous forme littérale, l'équation de la trajectoire. x = v0 cos a t ; t = x/(v0 cos a) ; y = -½gt2 + v0 sin at + h y = -½g[x/(v0 cos a)]2+ tan a x + h Quelle est la nature de la trajectoire ? branche de parabole. Montrer que pour la valeur a =45°, le carré de la vitesse initiale peut se mettre sous la forme : v02=gD2/(D+h) ; D est la distance entre l'origine O et le point d'impact au sol. Au sol : y = -½g[D/(v0 cos a)]2+ tan a D + h = 0 cos2 a =0,5 ; tan a = 1 ; 0 = -gD2 / v02 + D+h=0 ; gD2 / v02 = D+h ; v02 =gD2 /(D+h) CalcuIer l'énergie cinétique initiale ECO1 du cochonnet lorsque D est égal à 8 m et a à 45°. ECO1 = ½m v02 =½mgD2 /(D+h) = 0,5 * 15 10-3 *10*64/10=1,5 *0,64/2 =0,48 J. Calculer l'énergie cinétique initiale EC02 de la boule de pétanque pour que, lancée du même point A, avec le même angle a = 45°, elle atteigne le cochonnet. calcul identique en remplaçant 15 g par 700 g. ECO1 = ½M v02 =½MgD2 /(D+h) = 0,5 * 700 10-3 *10*64/10=0,7 *64/2 =22,4 J. Les énergies cinétiques de la boule de pétanque et du cochonnet sont différentes lorsqu'ils atteignent Ie sol. Qu'en est-il des vitesses de chacun ? Energie mécanique initiale du cochonnet : mgh + ½m v02 Energie mécanique finale du cochonnet : ½m v2 conservation de l'énergie mécanique : mgh + ½m v02 = ½m v2 ; v2 =v02 + 2gh. La vitesse finale est indépendante de la masse : le cochonnet et la boule lancés dans les mêmes conditions initiales, ont la même vitesse finale.

retour -menu