Régimes transitoires électriques concours kiné Nantes 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

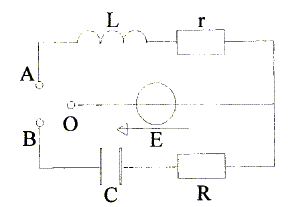
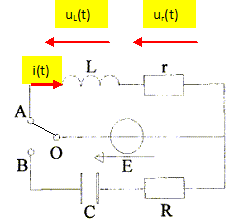
Rappel : si x est une grandeur fonction du temps satisfaisant à l'équation différentielle t dx(t)/dt + x(t) = H où t et H sont constants, x(t) est de la forme générale : x(t) = K exp(-t/t) + H. K est une constante que l'on détermine en considérant les conditions initiales. On réalise le montage ci dessous : Le générateur est une source idéale de tension de fem E = 6,0 V. A t = 0 on relie les points O et A. Représenter le circuit parcouru par le courant i(t), et noter les tensions uL(t) aux bornes de l'inductance L et ur(t) aux bornes de la résistance r. Etablir l'équation différentielle relative à i(t). Additivité des tensions : uL(t) + ur(t) = E. Ldi(t)/dt + r i(t) = E. L/r di(t)/dt + i(t) = E / r. Préciser les valeurs de l'intensité i(t) aux dates t=0 et t très grand ( régime permanent ). A la date t0-, la bobine ne stocke pas d'énergie : i(t0-) =0. La continuité de l'intensité conduit à : i(t0+) =0 : donc i(t=0) = 0. En régime permanent, l'intensité est constante et di(t)/dt = 0, d'où i(too) = E/r. Déterminer la constante de temps t1 en fonction de L et r et donner l'expression littérale de i(t). t1 = L/r ; i(t) = K exp(-t/t1) + E/r ; i(0) = 0 = K + E/r soit K = -E/r. i(t) = E/r ( 1-exp(-t/t1). 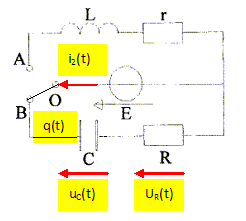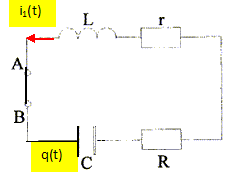On coupe la connexion entre O et A. Le condensateur étant déchargé, on relie O à B à un instant choisit comme nouvelle origine des temps. Représenter le circuit parcouru par le courant i2(t) ; noter la charge q(t) du condensateur de capacité C, la tension uC(t) aux bornes du condensateur et la tension uR(t) aux bornes du conducteur ohmique de résistance R. 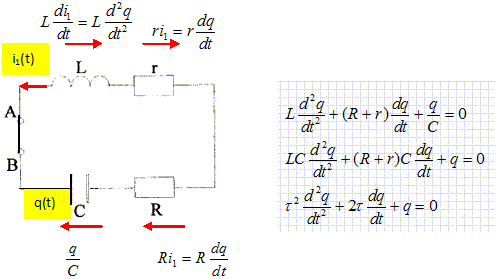Etablir l'équation différentielle relative à q(t). Additivité des tensions : uC(t) + uR(t) = E. q(t) / C + R i2(t) = E avec i2(t) = dq(t) / dt : q(t) / C + R dq(t) / dt = E RC dq(t)/dt + q(t) = CE. Préciser les valeurs de la charge q(t) aux dates t=0 et t très grand ( régime permanent ). A la date t0-, le condensateur ne stocke pas d'énergie : q(t0-) =0. La continuité de la charge conduit à : q(t0+) =0 : donc q(t=0) = 0. En régime permanent, la charge est constante et dq(t)/dt = 0, d'où q(too) = CE.   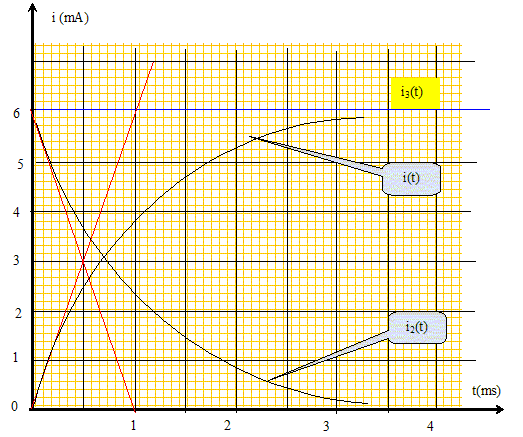Déterminer la constante de temps t2 en fonction de C et R et donner l'expression littérale de q(t). t2 = RC ; q(t) = K exp(-t/t2) + EC ; q(0) = 0 = K + EC soit K = -EC. q(t) = EC ( 1-exp(-t/t2). Donner l'expression littérale de i2(t). i2(t) = dq(t)/dt = EC / t2 exp(-t/t2) ; i2(t)= E/R exp(-t/t2). Le condensateur étant de nouveau déchargé, on relie à l'instant t=0, le point O à la fois à A et B. L'intensité débitée par le générateur de fem E est notée i3. Rappeler la loi des noeuds reliant à chaque instant i(t), i2(t) et i3(t). Au noeud O : i3(t) = i(t) + i2(t). Les expressions de i(t), i2(t) étant celles obtenues ci-dessus, donner l'expression littérale de i3(t). i3(t) = E/R exp(-t/t2) + E/r ( 1-exp(-t/t1)). i3(t) = E [ 1/R exp(-t/t2) - 1/r exp(-t/t1) + 1/r].   Exprimer les conditions que doivent vérifier les valeurs associées aux composants pour que i3(t) soit indépendant de t. 1/R exp(-t/t2) - 1/r exp(-t/t1) doit être nulle. d'où : R = r et t1= t2 ; L/r = RC ; L = rRC ; L= R2C. A.N : C = 1,0 µF et R = 1,0 kW. par suite : r = 1,0 kW ; L = 106*10-6 = 1,0 F. Tracer sur le même graphique i(t), i2(t) et i3(t) avec les tangentes à l'origine. t1= t2 = 10-3 s = 1 ms ; i(t) = 6/1000 ( 1-exp(-t))= 6(1-exp(-t)) avec i en mA et t en ms. i2(t) = 6 exp(-t) avec i2 en mA et t en ms. i3(t) =6 exp(-t) + 6 ( 1-exp(-t) ; i3(t)=6 mA. Les valeurs des composants étant celles calculées précédemment, on réalise une nouvelle expérience. Après avoir chargé le condensateur au maximum ( charge q = Q0), on relie à l'instant t = 0, le point B au point A ( C, L, R et r sont en série). Représenter le circuit parcouru par le courant i1(t) ; noter la charge q(t) du condensateur de capacité C. Montrer que la constante de temps s'exprime par t1 = (LC)½. On notera par la suite t = (LC)½. t1 =L/r = L/R et L = R2C ; R = L½ C-½ ; par suite : t1 = L½C½. Ecrire l'équation différentielle relative à q(t) où l'on fera apparaître t .   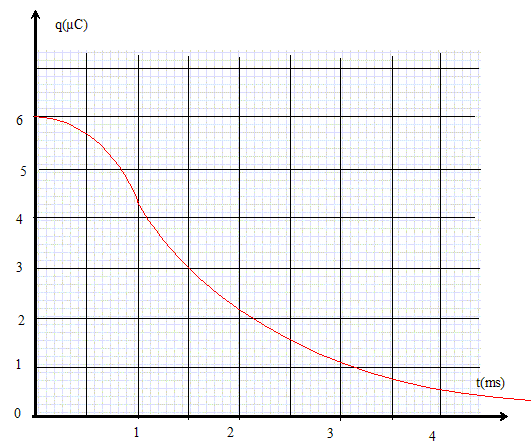Le régime est alors dit apériodique critique. q(t) est de la forme q(t) = (a+ßt) exp(-t/t) où a et ß sont des constantes. Préciser les valeurs de la charge q et de l'intensité i1 à t=0 ; en déduire l'expression de q(t). Le condensateur est chargé au maximum à t = 0 : q(0) = Q0 = CE = 6 10-6 C = 6 µC. La bobine ne stocke pas d'énergie à t = 0 : i(0) = 0. q(0) = a exp(0) = a = CE = 6 µC. i1(t) = dq/dt = ß exp(-t/t) + (a+ßt) (-1/t ) exp(-t/t) i1(0) = 0 = ß- a/t = 0 ; ß = a/t = CE ( LC)-½ = 6 10-6 (1*10-6)-½ ; ß = 6 10-3 C s-1. ( LC)½ = (1*10-6)½ = 10-3 s = 1 ms. q(t) = 6 (10-6+10-3 t ) exp(-1000t) = 6 10-6 (1 +1000t)exp(-1000t) q(t) = 6(1+t) exp(-t) avec q en µC et t en ms.

c

retour -menu