Radioactivité alpha, onde sur une corde concours kiné Nantes 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Le bismuth 212, 21283Bi est un radionucléide de type alpha ; sa désintégration conduit à un nucléide du thalium de symbole Tl. Ecrire l'équation de désintégration. 21283Bi ---> AZTl + 42He Conservation de la charge : 83 = 2+Z d'où Z = 81. Conservation du nombre de nucléons : 212 = 4 + A d'où A = 208 21283Bi ---> 20881Tl + 42He. Cette désintégration s'accompagne d'émission d'un rayonnement g. Expliquer cette émission de photons g. Le noyau fils20881Tl est dans un état excité ; il revient à l'état fondamental en cédant de l'énergie au milieu extérieur sous forme de photons g. Calculer la fréquence et l'énergie du photon de longueur d'onde l = 2,00 pm ( 1 pm = 10-12 m). c = 3,00 108 m/s ; h = 6,63 10-34 Js. n = c / l = 3,00 108 / 2,00 10-12 = 1,50 1020 Hz. E = h n = 6,63 10-34*1,50 1020 =9,95 10-14 J. Comparer cette énergie avec celle des photons de la lumière visible ayant la plus grande énergie. Conclure. Les longueurs d'onde de la lumière visible sont comprises entre 400 nm et 750 nm. L'énergie d'u photon est d'autant plus grande que sa longueur d'onde est plus petite. E = h c / l = 6,63 10-34*3,00 108 / 400 10-9 =4,97 10-19 J. Cette valeur est 200 000 fois plus petite que l'énergie du photon g : ce dernier est donc extrèmement dangereux pour la matière vivante. Onde se propageant sur une corde. 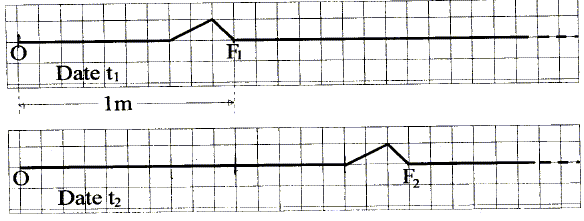Un dispositif permet de générer à l'extrémité O de la corde tendue horizontalement une déformation qui se propage le long de cette corde. On néglige les phénomènes d'amortissement et de réflexion. La corde est représentée ci-dessous aux dates t1 et t2. Déterminer la célérité de propagation de la déformation si t2-t1 = 20 ms. F1F2 = 0,80 m d'après la figure ; t2-t1 = 0,020 s c = F1F2 / (t2-t1)=0,80 / 0,020 = 40 m/s. L'origine des dates correspond au début de la déformation transversale en O. Déterminer la date t1. D'après la figure, le front de la perturbation a parcouru 1 m à la date t1, à la célérité de 40 m/s. t1 = 1 / 40 = 0,025 s = 25 ms. Représenter la corde à la date t3 = 35 ms. Le front de la perturbation a parcouru la distance : 40*0,035 = 1,4 m.   La célérité de l'onde le long de la corde tendue est donnée par la relation v = (T/µ)½. T : tension de la corde ; µ : masse linéique = 5,0 g m-1. Calculer T. T = v2µ avec µ = 5,0 10-3 kg m-1. T = 402 *5,0 10-3 = 8,0 N. L'extrémité de la corde est maintenant reliée à un vibreur produisant une onde sinusoïdale transversale de fréquence 100 Hz le long de la corde. Calculer la longueur d'onde l. l= v / f = 40/100 =0,40 m = 40 cm. Donner l'allure de la corde lorsque le front d'onde F est à la distance OF = 100 cm. 100 cm = 2,5 *40 = 2,5 l. A l'instant initial, la déformation peut se faire vers le haut ou vers le bas.

c

retour -menu