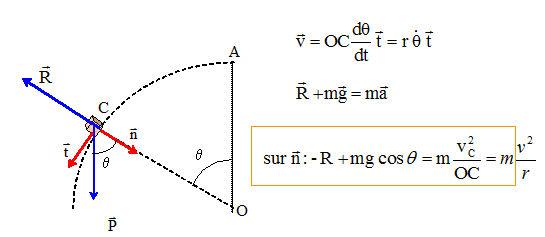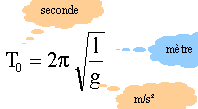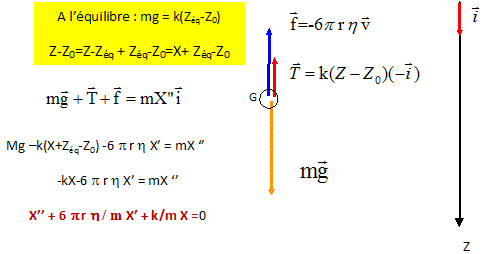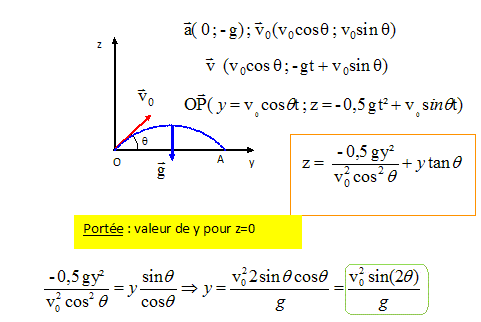QCM mécanique : oscillateur, projectile, chute... ( Kiné St Michel 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Bille sur une sphère. Données :Sur une qphère de centre O, de rayon r, une bille de masse m est lachée sans vitesse initiale du point A situé sur la verticale passant par O. Cette bille, très petite peut être considérée comme un point matériel M glissant sans frottement sur la sphère. La bille est repérée par l'angle q. Analyse : les vecteurs sont écrits en gras et en bleu. A- Dans le repère de Frenet (C, t, n) le vecteur vitesse s'écrit v = r q' t. Vrai. B- Dans le repère de Frenet (C, t, n) le vecteur accélération s'écrit a = r q " t. Faux. C- La vitesse de la bille à chaque instant est donnée par la relation : v2 =2gr(1-cosq). Vrai. variation de l'énergie cinétique : ½mv2-0. travail moteur du poids en descente : mgr( 1-cosq) ; R perpendiculaire à la vitesse ne travaille pas. Ecrire le théorème de l'énergie cinétique entre A et C : ½mv2= mgr( 1-cosq) D- La réaction R de la sphère sur la bille est donnée par : R=mg(2+3cosq). Faux. R = mg cos q -mv2/r avec v2 / r =2 g( 1-cosq) R = mg [ 3cos q -2 ] Satellite géostationnaire. Analyse : A- Sa période de révolution est T0 = 86184 s. Vrai. période de révolution t égale à la période de rotation de la Terre sur elle-même (23 heures 56 minutes et 4,1 secondes). B- Il se déplace dans le plan de l'ecliptique. Faux. Il se déplace dans le plan de l'équateur. C- Il est fixe dans le référentiel géocentrique. Faux. Il paraît fixe pour un observateur terrestre. D- Il tourne dans le même sens que la terre. Vrai. Balancier d'une horloge ancienne. Le balancier d'une horloge ancienne est généralement métallique. Si la température augmente, il se dilate et sa longueur augmente. On assimilera le balancier à un pendule simple. Analyse : si le pendule bat la seconde, alors la période est T0=2s. A : Si la longueur augmente, la période propre diminue. Faux. La période est proportionnelle à la racine carrée de la longueur. B : En été cette horloge avance. Faux. La période augmente car la longueur du pendule augmente : l'horloge retarde. C : En hiver l'horloge retarde. Faux. La période diminue car la longueur du pendule diminue : l'horloge avance. D : La période de cette horloge maintenue à température constante dans une enceinte, augmente lorsqu'on la transporte du bord de la mer au sommet d'une montagne. Vrai. Au sommet d'une montagne g est inférieur à sa valeur en bord de mer : donc la période augmente. Sphère plongée dans un liquide Les vecteurs sont écrits en gras et en bleu. Une sphère de rayon r est animée d'une vitesse v dans le référentiel terrestre. Plongée dans un liquide de viscosité h , elle est soumise à une force de frottementqui, pour une vitesse faible, est opposée au vecteur vitesse et a pour expression : f = -6p r h v. Cette sphère est suspendue à un ressort de raideur k. Sa période d'oscillation dans l'air, ou le frottement est négligeable est T0. On la plonge dans le liquide de viscosité h. On pose 2l = 6p r h / m et w02 = k/m. L'équation différentielle en X du mouvement en prenant pour origine la position d'équilibre de la sphère ( X = Z-Zéqui avec Z axe verticale descendant d'origine le point d'accrochage du ressort) est : A B C( vrai) D X"+2lX'-w02X=0 X"-2lX'-w02X=0 X"+2lX'+w02X=0 X"-2lX'-w02X=0 Analyse : Oscillateur horizontal. UnOscillateur est constitué d'un objet ponctuel M de masse m = 0,20 kg fixé à l'extrémité d'un ressort idéal de constante de raideur k = 5,0 N/m, enfilé sur une tige horizontale. Le tout coulisse sans frottement. L'origine des abscisses est la position M0 de l'objet lorsque le ressort est détendu. On désigne par X, l'abscisse de l'objet M à un instant de date t quelconque. Elle est repérée sur un axe x'x de même direction que la tige. A l'origine des dates M est en M0, sa vitesse a pour valeur 0,60 m/s et elle est dirigée dans le sens négatif de l'axe. L'équation horaire décrivant le mouvement est : A B C( vrai) D X = 0,060 cos ( 5t) X = 0,12 cos ( 5t) X = 0,12 cos ( 5t + ½p) X = 0,12 cos ( 5t - ½p) Analyse : L'équation horaire est du type : X = A cos ( wt+F) w = (k/m)½ = (5/0,2)½ =25½ = 5 rad/s. A, amplitude, constante positive non nulle et F une constante. A la date t=0, X(0) =0 = A cos F soit cos F = 0 : il y a deux possibilités F = ½p ou F = -½p. Vitesse , dérivée de X par rapport au temps : X' = -5A sin ( 5t+F) A la date t=0, X'(0) = -0,60 = -5A sin F ; d'où F=½p et A = 0,12 m.   Projectile. Unsolide est lancé vers le haut dans une direction faisant un angle de 45 ° avec la verticale. Les frottements dus à l'air sont négligeables. Analyse : A : le centre d'inertie G du solide repasse par sa position initiale. Faux. B : Le vecteur vitesse de G change d'orientation. Vrai. C : Le vecteur accélération de G change d'orientation au cours du mouvement. Faux. D : La vitesse s'annule au sommet de la trajectoire. Faux. Seule la composante verticale s'annule au sommet ; la composante horizontale n'est pas nulle. E : L'accélération s'annule au sommet de la trajectoire. Faux. Ascenceur. Arthur prend l'ascenceur en tenant son sac de sport à la main celui-ci ne touchant pas le sol. Pour Arthur, le sac paraît plus léger qu'à l'arrêt : Analyse : Dans un référentiel lié au sol : A : lorsque l'ascenseur démarre en montant. Faux. a >0 ; F= ma+mg est supérieure au poids ; la personne a l'impression d'être plaquer au sol. B : lorsque l'ascenseur démarre en descendant. Vrai. a >0 ; F= mg-ma est inférieure au poids ; la personne a l'impression de " décoller" C : lorsque l'ascenseur monte à vitesse constante. Faux. L'accélération est nulle et F = mg. D : lorsque l'ascenseur ralentit en montant. Vrai. a <0 ; F= ma+mg est inférieure au poids. E : lorsque l'ascenseur ralentit en descendant. Faux. a <0 ; F= mg-ma est supérieure au poids. Portée d'un projectile. Un projectile est lancée avec une vitesse v0 = 50 m/s d'un point O situé au sol Pour atteindre un point A situé au sol à une distance L= 1,25 m m du point O, l'angle de tir doit être égal à : A B C D E ( vrai) 30° 75° 45° 60° 15° Analyse : sin (2q) = gy/v02 =10*125 / 502 = 0,5 ; 2q = 30 ° ; q = 15 °

retour -menu