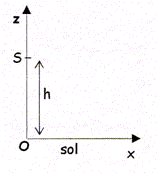
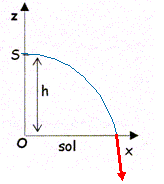
Constante d'équilibre, électrolyse, radioactivité, chute libre : concours manipulateur radio ( St Germain 2008) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Dans un volume V = 100 mL on a mis en solution une quantité n0 = 1,0 10-3 mol/L des espèces suivantes : acide nitreux HNO2 (aq), nitrite de sodium ( Na+(aq) + NO2-(aq)), acide fluorhydrique HF(aq) et fluorure de sodium (Na+(aq) + F-(aq)). La transformation qui se produit est modélisée par l'équation chimique : HNO2 (aq) +F-(aq) = HF(aq) +NO2-(aq) ; constante d'équilibre K = 0,74. Ecrire l'expression littérale de cette constante d'équilibre. K =[HF(aq)]éq[NO2-(aq)]éq / ( [F-(aq)]éq [HNO2 (aq)]éq ) Calculer le quotient initial de réaction. Q r i =[HF(aq)]i[NO2-(aq)]i / ( [F-(aq)]i [HNO2 (aq)]i ) = 1. Toutes les espèces ont initialement la même concentration. Dans quel sens évolue la réaction. Justifier. Q r i est supérieur à K, le critère d'évolution spontané indique une évolution dans le sens indirect, vers la gauche. Etablir un tableau d'avancement et exprimer la constante d'équilibre en fonction de l'avancement final xf . 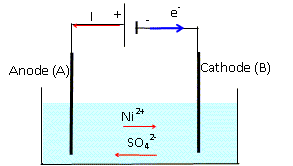avancement (mol) HNO2 (aq) +F-(aq) = HF(aq) +NO2-(aq) initial 0 n0 = 10-3 n0 = 10-3 n0 = 10-3 n0 = 10-3 en cours x n0 -x n0 -x n0 +x n0 +x équilibre xf n0 -xf n0 -xf n0 +xf n0 +xf [HF(aq)]éq= [NO2-(aq)]éq = (n0 +xf) /V ; ( [F-(aq)]éq = [HNO2 (aq)]éq = (n0 -xf) /V ; K = (n0 +xf)2 / (n0 -xf)2. Le nickel métallurgique obtenu à partir du minerai contient des impuretés. On le purifie par électrolyse. L'électrolyte utilisé est une solution de sulfate de nickel. Une des électrodes A est la plaque de nickel à purifier. L'autre électrode B est une plaque de nickel pur. Pendant l'électrolyse, le nickel contenu dans A s'oxyde et disperse ses impuretés dans la solution électrolytique. La réaction qui a lieu dans l'électrolyseur est : Ni(s) + Ni2+(aq) = Ni(s) + Ni2+(aq) Le générateur débite un courant d'intensité I supposée constante, de valeur 2,0 A sous une tension de 4,0 V pendant 5 heures. Ecrire les demi-équations des réactions ayant lieu aux électrodes A et B dans le sens où elles se produisent. A, anode, oxydation du nickel : Ni(s) = Ni2+(aq) + 2e-. B, cathode, réduction de Ni2+(aq) : Ni2+(aq) + 2e- = Ni(s). Faire un schéma du dispositif en indiquant le sens du courant, le sens de circulation des électrons et les bornes du générateur. Justifier. L'anode, le nikel impur est relié à la borne positive du générateur ; à cette électrode le nikel impur s'oxyde. Etablir l'expression littérale entre la quantité de matière de nickel qui s'oxyde et les données du texte. Calculer sa valeur. Aide au calcul : F=96500 C; 5*36/965 = 0,18. Quantité de matière d'électricité : Q= I t avec I= 2,0A et t = 5*3600 s Quantité de matière d'électrons : n = Q/F = I t / F Quantité de matière de nickel (mol) : n(Ni) = ½n = ½I t / F n(Ni) = 0,5*2,0*5*3600/96500 = 0,5*2*0,18 = 0,18 mol. Le nucléide 22994Pu du plutonium peut réagir avec un neutron selon la réaction : 22994Pu + 10n --> 135ZTe + A42Mo + 310n. Masses des nucléides en MeV/c2 : m(22994Pu) =222,655 103 ; m( 10n) =932 ; m(135ZTe) =125,662 103 ; m(A42Mo) =94,920 103. Masse atomique molaire de 22994Pu : M =239 g/mol ; NA = 6 1023 mol-1 ; 1 MeV/c2 =1,6 10-13 J ; 209*1,6 = 330 ; 209/1,5 = 130. Cette réaction est-elle une fusion ou une fission. Justifier. Un noyau lourd instable se casse ne deux noyaux plus légers et plus stables : donc fission. Enoncer les deux lois de conservation et déterminer A et Z. Conservation de la charge : 94 = Z +42 ; Z = 52. Conservation du nombre de nucléons : 229+1 = 135+A+3 ; A = 92. Vérifier que la perte de masse de cette réaction est égale à -209 MeV/c2 . Détailler le calcul. Dm = 2 m( 10n) + m(135ZTe) + m(A42Mo) -m(22994Pu) Dm = 2*932+103(125,662 +94,920-222,655) = -209 MeV/c2. Que vaut en MeV et en Joule l'énergie libérée. E = 209 MeV ou 209*1,6 10-13 = 330 10-13 = 3,3 10-11 J.   Lors d'une mission humanitaire, un avion volant horizontalement à l'altitude h = 3,0 103 m, à vitesse constante v0, largue en un point S, un colis de vivres. La résistance de l'air est négligeable devant le poids, le poids est donc la seule force qui s'exerce sur le colis. g = 10 m s-2 ; 6½ =2,4 ; 3½ = 1,7. Dans le référentiel terrestre quelle est la valeur de la vitesse initiale du colis ? v0. Donner les coordonnées des vecteurs accélération et vitesse. accélération ( 0 ; -g ) ; vitesse ( v0, -gt) En déduire les équations horaires x(t) et z(t) du mouvement du colis dans le repère ( 0, x, z). x(t) = v0t ; z(t) =-½gt2 +h. En déduire l'équation de la trajectoire ; de quel type de courbe s'agit-il ? La reproduire sur le dessin. Représenter le vecteur vitesse lorsque le colis touche le sol ( donner une longueur quelconque au vecteur) t =x(t) / v0 ; z(t) = -½g x2 / v02 + h. Le vecteur vitesse est tangent à l'arc de parabole en x=0 ( sol). Calculer la durée au bout de laquelle le colis touche le sol. z(t) =-½gt2 +h = 0 au sol ; t2 = 2h/g = 2*3,0 103 / 10 = 6 102 ; t = 2,4*10 = 24 s.

retour -menu