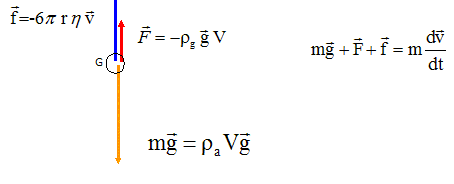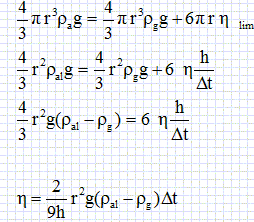Chute d'une bille dans la glycérine ( Kiné Berck 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

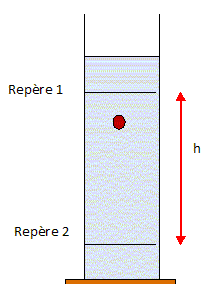
Une bille sphérique en acier, de rayon r est lâchée sans vitesse initiale dans une éprouvette contenant de la glycérine. Lorsque la bille passe devant le repère n°1 elle a déja atteint sa vitesse limite de chute vl. Une caméra couplée à un ordinateur permet de mesurer la durée de la chute de la bille entre les deux repères. Le début de cette mesure commence lorsque le bas de la bille est tangent au trait du repère 1 et s'arrête lorsque le bas de la bille est tangent au trait repère 2. la durée de la chute de la bille entre les deux traits est notée Dt. On réalise deux mesures de temps de chute en prenant la glycérine à deux températures différentes : - pour q1 = 15,0°C on trouve D t1 =20,9 s - pour q2 = 20,0°C on trouve D t2 =13,3 s. Les grandeurs écrites en gras et en bleu sont des vecteurs. Au cours de la chute la bille est soumise aux forces suivantes : - son poids P, la poussée d'Archimède F exercée par la glycérine, la force de frottement fluide modélisée par f = -kv avec k = 6prh ( h viscosité dynamique de la glycérine en Pa s). Données : h = 80,0 cm ; r = 2,50 mm masse volumique de l'acier ra =7,85 g cm-3 ; masse volumique de la glycérine rg =1,29 g cm-3 . Représenter sur un schéma les forces qui s'exercent sur la bille lors de la chute. Donner l'expression de la vitesse limite en fonction de h et Dt.  vl = h / Dt. Etablir l'expression de la viscosité dynamique en fonction de g, r, h, Dt, ra et rg.   Calculer les valeurs de la viscosité dynamique aux deux températures 15 °C et 20 °C. r = 2,5 10-3 m ; ra - rg =(7,85-1,29) 103 = 6,56 103 kg m-3 ; h = 0,80 m h =2*(2,5 10-3)2 *9,81 * 6,56 103 / (9*0,8) Dt = 0,11172 Dt . h1 =0,11172*20,9 = 2,3350 ~ 2,33 Pa s. h1 =0,11172*13,3 =1,4859 ~1,49 Pa s.   La viscosité dynamique dépend de la température et vérifie ,dans les conditions de cette expérience, la loi de Guzman-Andrade qui s'écrit : h = A exp(B/T) avec A et B deux constantes à déterminer et T la température en kelvin. Déterminer la viscosité dynamique h3 à 30,0°C. h1 = A exp (B/ (273+15)) ; 2,335 = A exp (B/288) = A exp(0,003472 B) 1,4859 = A exp (B/293) = A exp (0,003413 B) 2,335/1,4859 =1,571 = exp((0,003472-0,003413)B) =exp(5,9 10-5 B) B = ln (1,571 )/ 5,92 10-5 =7,63 103 K A = 1,4859 / exp(7,63 103 /293) =7,3 10-12 Pa s. h3 =7,3 10-12 exp((7,63 103 /303) = 0,63 Pa s. En déduire la durée de la chute à cette température. h == 0,11172 Dt ; Dt = 0,63 / 0,11172 = 5,6 s.

retour -menu