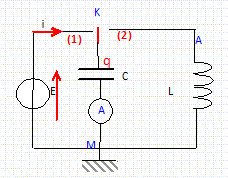
condensateur : capteur de sonde d'humidité ( Kiné Berck 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Le pourcentage d'humidité relative P de l'air est le rapport exprimé en pourcentage, de la quantité de vapeur d'eau contenue dans un certain volume d'air à la quantité correspondant à la saturation dans les conditions considérées. L'air parfaitement sec a un pourcentage d'humidité relative P = 0% et l'air complètement saturé d'humidité P = 100 %. Le capteur de certaine sonde d'humidité est composé d'un condensateur plan dont la capacité C varie en fonction de ce pourcentage d'humidité relative. On dispose d'un condensateur de ce type dont les caractéristiques sont données : - la capacité est une fonction affine du pourcentage d'humidité relative P - gamme d'utilisation : 10 % <P <90% ; sensibilité du capteur s = dC/dP. On réalise le circuit ci-dessous : étape 1 : l'interrupteur K est en position 1 pendant le temps nécessaire pour que le condensateur se charge complètement. étape 2 : on bascule l'interrupteur en position 2. Le circuit est le siège d'oscillations électriques libres et d'amortissement négligeable. On suit alors l'évolution de l'intensité i dans le circuit. On détermine la fréquence f des oscillations et la valeur maximale de l'intensité Imax. On réalise une première mesure et on trouve Imax = 14,2 mA ; f = 1,12 kHz avec E = 12,0 V. Déterminer la capacité C1 ( en nF) du condensateur lors de cette mesure. Expression de la charge du condensateur : q = C1E cos ( 2pft). Expression de l'intensité : i = dq/dt = - C1E2pf sin ( 2pft). Imax =C1E2pf ; C1 = Imax /(E2pf) = 14,2 10-3 / (12*2*3,14*1120) =1,68 10-7 F =168,15 10-7 F = 168 nF. En déduire la valeur de l'inductance L de la bobine. f = 1/(2p(LC)½) ; L = 1/(4p2C f2) = 1/(4*3,142 *1,68 10-7 *11202) =0,12 H. On considère que l'inductance est constante au cours des mesures réalisées. On effectue les mesures suivantes dans les mêmes conditions de température et de pression que la première mesure. le pourcentage d'humidité est lu sur un hygromètre.   Mesure P ( %) Imax( mA) f(kHz) n°2 30,4 13,7 1,16 n°3 54,8 14,9 1,07 la capacité C du condensateur varie en fonction de P selon la relation : C = aP+b où a et b sont des constantes. C est en nF et P en %. Déterminer les valeurs des constantes a et b. C = 1/(4p2L f2) ; C2 = 1/(4*3,142 *0,12 *11602) =156,87 ~157 nF. C3 = 1/(4*3,142 *0,12 *10702) =184,37~184 nF. 156,87 = 30,4 a + b (2) ; 184,37 = 54,8 a+b (3) (3) -(2) : 184,37-156,87 = (54,8-30,4) a ; a = 1,127 ~a = 1,13 nF %-1; b = 123 nF. (122,6) En déduire la valeur de la sensibilité s ( en nF / %) du condensateur. s = dC/dP = a = 1,13 nF %-1. Déterminer la valeur P1 du pourcentage d'humidité lors de la première mesure. C1 = 1,13 P1 +123 ; P1 = (C1 -123) / 1,13 = (168,15-122,6) / 1,127 = 39,8%. On injecte 5,0 mL d'une solution contenant une substance radioactive d'activité A0 = 185 kBq dans le corps d'un chien endormi. 20 heures après l'injection, on effectue un prélevement de 25 mL de sang. La mesure de l'activité donne : A = 1,14 kBq. On suppose que la substance radioactive sest diffusée de manière homogène dans tout le sang de l'animal. Demi-vie de la substance t½ = 15 h. Calculer le volume total ( en L) de sang dans le corps du chien. A B C D ( vrai) E F 1,0 1,2 1,4 1,6 1,8 autre Analyse : Loi de décroissance radioactive A = A0 exp(-lt) avec l = ln2 / t½ = ln2 / 15 = 4,62 10-2 h-1. Activité dans tout le sang au bout de 20 h : A = 185 exp(-4,62 10-2*20) =73,42 kBq Volume de sang : 25*73,42 / 1,14 =1,6 103 mL = 1,6 L.     On considère un noyau de lithium 73Li dont la masse vaut mLi = 7,0144 u. 1 u = 1,66054 10-27 kg ; masse du neutron mn=1,00866 u ; masse du proton mp=1,00728 u ; 1 eV = 1,6022 10-19 J ; c = 2,9979 108 m/s. Combien y a-t-il de propositions exactes ? A- la masse de ce noyau est supérieure à la somme des masses des nucléons qui le constituent. Faux. B- le défaut de masse de ce noyau est 6,9876 10-28 kg. Faux. 3 mp + 4mn -mLi =3*1,00728 +4*1,00866-7,0144 =4,208 10-2 u 4,208 10-2 *1,66054 10-27 =6,9876 10-29 kg C- le défaut de masse peut s'exprimer en MeV/c2. Vrai. D- l'énergie de liaison par nucléon de ce noyau est 5,60 MeV/nucléon. Vrai. Dm c2 =6,9876 10-29 *(2,9979 108)2 =6,28 10-12 J 6,28 10-12 /1,60 10-19 =3,92 107 eV = 39,2 MeV puis diviser par le nombre de nucléons : 39,2/7 = 5,6 MeV/nucléon. E- le noyau de lithium peut s'unir avec un autre noyau léger pour former un noyau plus lourd : il s'agit de la fission nucléaire. Faux. fusion nucléaire.

retour -menu