Circuit LC : énergie, équation différentielle concours kiné Assas 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

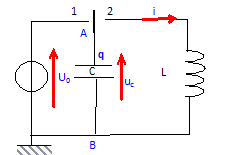
On a chargé un condensateur de capacité C= 1,0 µF sous une tension constante U0 = 10 V et on le branche aux bornes d'une bobine pure d'inductance L= 10 mH. Donner les expressions littérales des énergies électrostatique El(t) et électromagnétique Em(t) stockées dans les dipôles à l'instant t. El(t)=½C uc2 = ½q2/(2C) ; Em(t) = ½L i2. Donner les expressions littérales de la charge maximale Qmax du condensateur et de l'intensité maximale Imax du courant circulant dans le circuit. Qmax = CU0. Il y a échange d'énergie entre condensateur et bobine de telle sorte que : ½Q2max / C=½LI2max ; I2max= Q2max / (LC)= C/L U20 Imax=( C/L)½ U0. 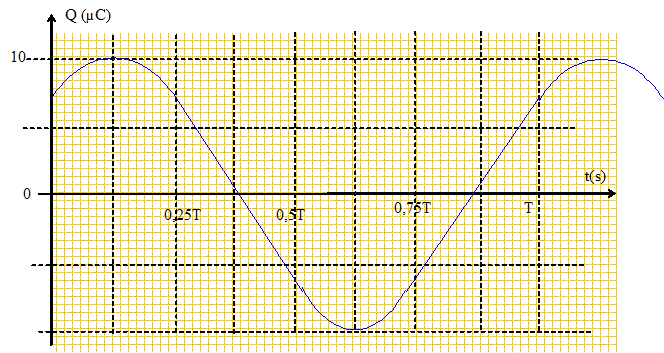A l'instant t=0, date du début de l'acquisition des données, l'énergie électrostatique est égale à l'énergie électromagnétique. A cet instant la charge de l'armature A du condensateur est positive et l'intensité est négative. Donner les expressions littérales de la charge initiale q0 et de l'intensité initiale I0 en fonction de Qmax et Imax. ½q20 / C=½LI20 et ½q20 / C+½LI20 =½Q2max / C = ½LI2max ; ½q20 / C+½q20 / C =½Q2max / C ; 2 q20 =Q2max d'où q0 = Qmax / 2½. De même : ½LI20 +½LI20 = ½LI2max ; I20 = ½I2max ; I0 = -Imax / 2½. A partir d'arguments énergétiques, trouver l'éqution différentielle vérifiée par q(t). A la date t, l'énergie est répartie entre condensateur et bobine. ½q2/C + ½Li2 = Constante (1) avec de plus i = -dq/dt = - q' en tenant compte du sens positif choisi pour l'intensité et i' = -q" = -d2q/dt2. Dériver (1) par rapport au temps : q q'/ C + L i i' = 0 soit q q' /C + L (-q') (-q") = 0 soit en divisant par q' : q/C +L q" = 0 ou encore q" + 1/(LC) q = 0.   La solution de cette équation différentielle est du type q(t) = A cos ( 2pt/T0 +j) avec T0 = 2p(LC)½. Donner l'expression littérale de i(t). i(t) = -q'(t) = A2p/T0sin ( 2pt/T0 +j) Donner les valeur de A et j. A t = 0, I0 = -Imax / 2½ et i(0) = A2p/T0sin ( j) -Imax / 2½ = A2p/T0sin ( j) D'une part : A est une amplitude, grandeur positive : A = ImaxT0 / (2p) A = Imax(LC)½ ; or Imax=( C/L)½ U0 A = C U0 = 10-6*10 = 1,0 10-6 C. d'autre part : sin ( j) = -1/ 2½ soit j = -p/4. 2p /T0 = (LC)-½ =(10-6*10-2)-½ = 104 rad/s. q(t) = 1,0 10-6 cos(104 t -p/4). Tracer le graphe de q(t).

c

retour -menu