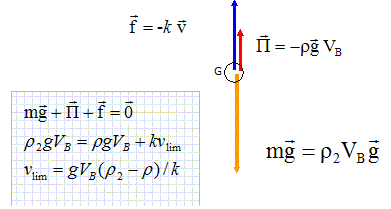Oscillateur mécanique, ondes sur une corde, chute dans un fluide, photon concours kiné AP HP 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Pendule simple. Un pendule simple de masse m = 10 g, de longueur L = 1 m est écarté de sa position d'équilibre d'un angle égal à 8 °. On le lâche sans vitesse initiale et on néglige les frottements. Le plan horizontal contenant la position d'équilibre, est choisi comme référence de l'énergie potentielle. On donne cos 8° = 0,99 et g ~ 10 m s-2. Analyse : période du pendule. A-la période du pendule est inversement proportionnelle à la racine carrée de sa masse. Faux. La période vaut T = 2 pi [L/g]½, indépendante de la masse. Analyse : vitesse maximale. B- vmax = (2Em/m)½ avec Em, énergie mécanique du pendule. Vrai. L'énergie mécanique initiale est sous forme potentielle de pesanteur : mg L ( 1-cos 8°) La vitese est maximale en passant à la position d'équilibre ; l'énergie mécanique est sous forme d'énergie cinétique : ½mv2max. Em = ½mv2max ; v2max = 2Em/m ; vmax = (2Em/m)½. Analyse : valeur de l'énergie mécanique. C- Em = 1 mJ. Vrai. Em = mg L ( 1-cos 8°) = 0,01*10*1 ( 1-0,99) =0,1*0,01 = 10-3 J = 1 mJ. D- la vitesse de la masse est égale à la moitié de sa vitesse maximale quand l'énergie cinétique est égale au quart de son énergie mécanique. Vrai. Em = 0,5 mv2max. Ec = 0,25 Em = 0,5 mv2 ; 0,25 * 0,5 mv2max= 0,5 mv2 ; 0,25 v2max =v2 ; v = 0,5 vmax. Ondes mécaniques. On attache une corde AB de longueur L = 4,0 m à l'extrémité d'un vibreur. Ce vibreur produit le long de la corde une déformation sinusoïdale de fréquence f = 100 Hz. La corde est maintenue horizontale. l'autre extrémité passe dans une poulie sans frottements. A l'extrémité libre du fil on attache une masse m = 200 g. Ainsi la tension de la corde est égale au poids de la masse. Un système permet d'éviter les réflexions des ondes sur l'extrémité libre. La célérité le long de la corde est v = (T/µ)½ où T est la tension de la corde et µ la masse linéique de la corde. On donne µ = 20 g cm-1. Analyse : tension de la corde. A-la tension de la corde s'exprime en kg m s-1. Faux. Force = masse * accélération = masse * longueur / temps2. la tension s'exprime en kg m s-2. Analyse : célérité de l'onde. B- la célérité de l'onde augmente avec la masse linéique de la corde. Faux. La célérité diminue quand µ augmente. Analyse : amortissement. C-la corde est le siège d'oscillations amorties. Faux. En absence de frottements, il n'y a pas d'amortissement. Analyse : longueur d'onde. D- la longueur d'onde est l = 10 cm. Faux. tension T = mg = 0,2*10 = 2 N ; µ = 2 103 g m-1 = 2 kg m-1. v =(T/µ)½ =(2/2)½ = 1 m/s ; l = v / f = 1/100 = 0,01 m = 1 cm.   Chute dans un fluide : Les vecteurs sont écrits en gras et en bleu. On considère trois billes sphériques homogènes de rayon identique, de même volume VB faites de trois matières différentes avec les masses volumiques respectives : r1 =900 kg m-3 ; r2 =110 kg m-3 ; r3 =1300 kg m-3. les trois billes sont lâchées sans vitesse initiale dans un fluide de masse volumique r =1000 kg m-3 de la même altitude correspondant à la surface libre du fluide. Les billes en mouvement dans le fluide sont soumises à une force de frottement f = -k v avec k coefficient identique pour les trois billes et v : vitesse du centre de la bille. Analyse : équation différentielle. A-le mouvement de la bille 1 est régi par l'équation différentielle : dv/dt + k / (r1VB) v =(1 -r / r1) g. Faux. La bille 1, de densité d = 0,9, inférieure à celle du fluide, ne coule pas mais flotte : sa vitesse initiale étant nulle, sa vitesse est donc nulle. Analyse : poussée d'Archimède. B- la poussée d'Archimède exercée sur la bille 1 est plus intense que la poussée exercée sur la bille 3. Faux. La poussée est proprotionnelle au volume du fluide déplacé ; la bille 1 flotte, son volume immergé est inférieur à VB . Analyse : quelle bille flotte ? C-aucune bille ne flotte. Faux. La bille 1, de densité d = 0,9, inférieure à celle du fluide, ne coule pas mais flotte Analyse : vitesse limite. D- la bille 3 admet une vitesse limite supérieure à celle de la bille 2. Vrai. La vitesse limite est d'autant plus grande que la masse volumique de la bille est plus élévée.   A propos d'une molécule : La liaison chimique entre deux atomes d'une molécule peut être modélisée par un ressort de constante de raideur k. La période propre de ce système est la même que celle d'un oscillateur élastique de constante de raideur k et de masse égale à la masse réduite µ = m1 m2 /(m1+m2), m1 et m2 représentant les masses des deux atomes constituant la molécule.  On donne : µ = 1,58 10-27 kg ; c = 3 108 m/s ; pi2~ 10 ; 1,22*1,58 = 2,3 ; 1,22/1,58 = 0,9 ; 1,58 / 1,22 = 1,09 ; 1,2*1,582 = 3 ; 1,2 / 1,582 = 0,5. Ce système peut entrer en résonance lorsqu'il est excité par des ondes électromagnétiques. Des mesures permettent de montrer que la molécule de fluorure d'hydrogène absorbe des ondes de longueur d'onde dans le vide de 2,5 µm. Analyse : domaine de l'onde absorbée. A-la molécule de fluorure d'hydrogène absorbe dans l'ultra-violet. Faux. Les longueurs d'onde dans le vide des UV sont inférieures à 0,4 µm. 2,5 µm appartient à l'infrarouge. Analyse : fréquence de l'onde. B- la valeur de la fréquence de la radiation absorbée par la molécule est 1,2 106 Hz. Faux. f = c / l = 3 108 / 2,5 10-6 =1,2 1014 Hz. Analyse : fréquence propre. C-la fréquence propre de l'oscillateur a pour expression f = 2 pi(µ/k)½. Faux. La période a pour expression T = 2 pi(µ/k)½. Analyse : coefficient de raideur k. D- k = 920 N m-1. Vrai. T2 = 4 pi2 µ/k ; k = 4 pi2 µ/T2 = 4 pi2 µ f2. k = 4*10 *1,58 10-27*1,22 1028 =4*1,58*1,22*100 = 4*2,3*100=920 N m-1.

c

retour -menu