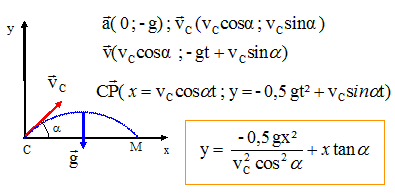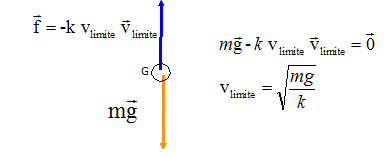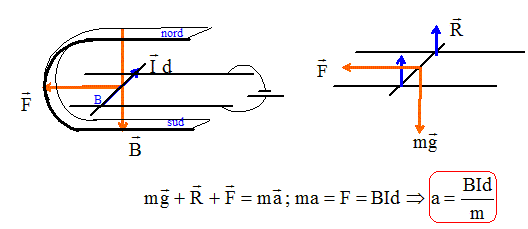|
accélération, chute libre, chute avec frottement, 3è loi de Kepler, pendule, force de Laplace concours kiné 2009.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
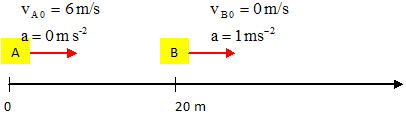
Analyse : mouvement de A. rectiligne uniforme xA = vA 0 t = 6 t. Analyse : mouvement de B. rectiligne uniformément accéléré : xB = ½at2 +20 = 0,5 t2 +20 Analyse : distance minimale AB. xB - xA = 0,5 t2 -6t + 20 La distance sera minimale si la dérivée est nulle : t-6 = 0 soit t = 6 s. xB - xA =0,5*62 - 6*6 +20 = 2 m. ( B) Analyse : nature
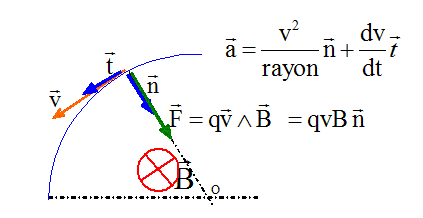
du mouvement. La force est à chaque instant
perpendiculaire à la vitesse : cette force
ne travaille pas et en conséquence ne
modifie pas l'énergie cinétique. La vitesse de la particule chargée garde
une valeur constante : mouvement
uniforme. La force est constante et est centripète
: mouvement circulaire. (
C)
Analyse : sommet de la trajectoire. Au sommet de la trajectoire, la vitesse est horizontale : la composante verticale de la vitesse est nulle. -gt + vC sin q = 0 ; t = vC sin q / g. A.N : vC = 10 m/s ; g = 10 m s-2 ; sin q =0,125 ; t = 0,125 s~0,13 s. (B)
Chute verticale avec frottements :
Analyse : vitesse limite. Lorsque la vitesse limite est atteinte, le mouvement est rectiligne uniforme. D'après le principe d'inertie, la somme vectorielle des forces est nulle. A.N : m = 40 g =0,040 kg ; g = 10 m s-2 ; k =
4,0 10-3 S.I ; vlimite = [
0,04*10/4,0 10-3]½=
10 m / s.
(A)
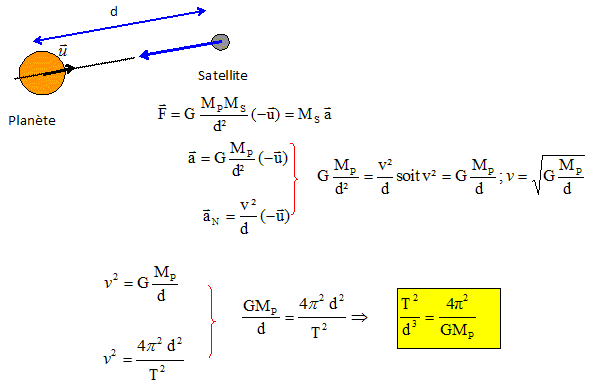
Analyse : masse de la planète. Par rapport à un référentiel planètocentrique galiléen : - la connaissance de l'accélération et du rayon de l'orbite circulaire permet de calculer la masse de la planète - la connaissance de la période de révolution et du rayon de l'orbite circulaire permet de calculer la masse de la planète. (E)
pendule simple :
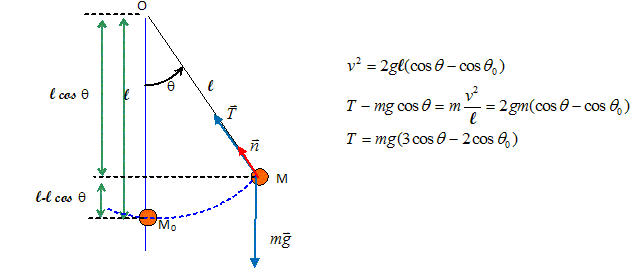
Analyse : tension du fil en M0. A la position M0, l'angle q est nu, cos q = 1 d'où T =mg(3-2 cosq0). (E) Oscillateur horizontal. Abscisse x(t) = xmax cos ( 2pf t) Vitesse, dérivée de l'abscisse par rapport au temps : v(t) = xmax (-2pf )sin ( 2pf t) Accélération, dérivée de la vitesse par rapport au temps : a(t) = -xmax (2pf )2 cos ( 2pf t) Valeur maximale de l'accélération : xmax (2pf )2 A.N : xmax =0,052 m ; f = 0,21 Hz ; a = 0,05 *(6,28*0,21) = 0,090 m s-2. (B)
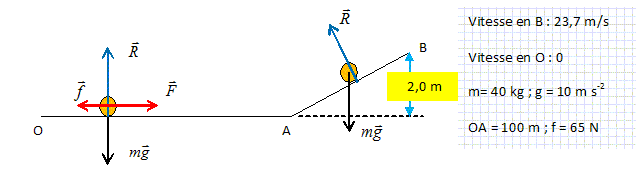
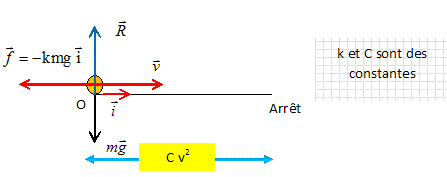
Distance de freinage.
Ecrire le théorème de l'énergie cinétique entre O et le point d'arrêt. Le poids et l'action du plan perpendiculaires à la vitesse ne travaillent pas. Travail résistant de la force de freinage f : Wf = -kmg Cv2. Variation de l'énergie cinétique : 0-½mv2. kmg Cv2 = ½mv2 ; kCg=½ ;
C = 1 / (2kg).
(E)
R = A1/3 avec A ; nombre de nucléons et R rayon du noyau en fm ( 10-15 m) Masse d'un nucléon : m = 2 10-27 kg. masse du noyau : M= A m (kg) volume du noyau supposé sphérique : 4/3 *3,14 (10-15R)3 = 4/3 *3,14 10-45 A (m3) masse volumique : M/V = 2 10-27 *3 / (4*3,14 10-45) ~5 1017 kg m-3. (D)
|
|||||||
|
c |
|||||||
|
|