Ondes sur une corde, diffraction, lentilles, dipôles RC et RL, photons, fusion nucléaire concours kiné 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

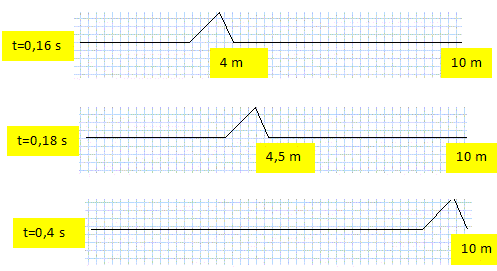
Onde transversale sur une corde tendue. Analyse : célérité v. v = (T/µ)½. T : tension de la corde ( N) ; µ : masse linéîque ( kg m-1). En doublant le diamètre de la corde : la section quadruple ; le volume et la masse par unité de longueur quadruplent ; la célérité est divisée par 2. Analyse : distance parcourue par la perturbation. Célérité : 0,5 / 0,02 = 25 m/s. Diffraction par une fente en lumière blanche. 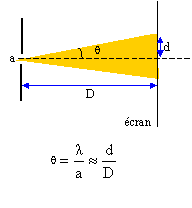Analyse : aspect de la tache centrale. La largeur de la tache centrale de diffraction est proportionnelle à la longueur d'onde. La lumière blanche est polychromatique : les longueur d'onde sont comprises entre 400 nm ( violet) et 800 nm ( rouge). La largeur de la tache centrale pour le rouge est la plus grande : on observe donc une tache blanche au centre ( toutes les couleurs de l'arc en ciel sont présentes ) , irrisée de rouge sur les bords. 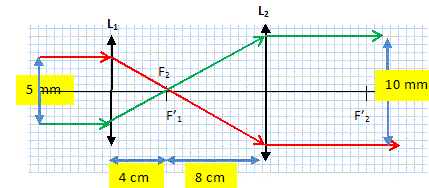(B) Lentilles : Analyse : allure du faisceau émergent. A un faisceau incident cylindrique correspond un faisceau émergent cylindrique dont le diamètre est égal à deux fois le diamètre du faisceau incident. 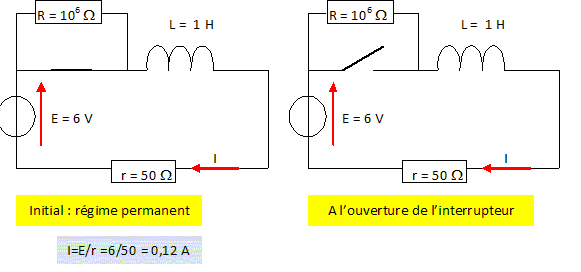(E) Ouverture de l'interrupteur d'un circuit inductif. A la date de l'ouverture de l'interrupteur : - continuité de l'intensité I = 0,12 A. - la tension aux bornes de l'interupteur présente un pic très important : RI =106*0,12 = 1,2 105 V. 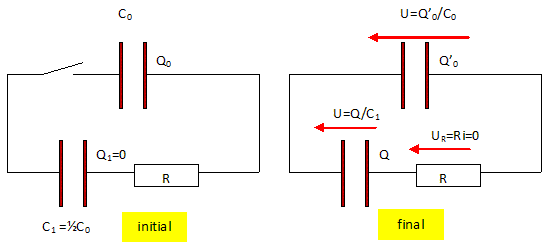(E) Décharge d'un condensateur à travers un dipôle RC. Analyse : conservation de la charge. Charge initiale : Q0 portée par le condensateur C0. Charge finale Q'0 pour le condensateur de capacité C0 et Q pour le condensateur de capacité C1. Q0 = Q'0 + Q (1). Analyse : tension finale aux bornes des condensateurs. U = Q'0 /C0 = Q/C1 avec C0 =2C1. Q'0 /(2C1 ) = Q/C1 ; ½Q'0 = Q Tenir compte de (1) : Q0 =3Q ; Q = Q0/3 ; Q'0 =2Q0/3 Analyse : énergie finale stockée par les condensateurs. Energie initiale stockée par le condensateur de capacité C0 : ½Q20/C0 Energie finale stockée par le condensateur de capacité C0 : ½Q'20/C0 =½(2Q0/3)2/ C0 = ½ 4Q02/(9C0). Soit 4/9 de l'énergie initiale. Energie finale stockée par le condensateur de capacité C1 : ½ Q2/C1 =Q2/C0= (Q0/3)2/ C0=Q02/(9C0)=½ *2Q02/(9C0) Soit 2/9 de l'énergie initiale. (A) Photons d'énergie 150 keV.   Analyse : longueur d'onde dans le vide. Energie exprimée en Joules :e = 1,5 105*1,6 10-19 = 2,4 10-14 J. l = hc/E. l =6,6 10-34 *3 108 / 2,4 10-14 =8,25 10-12 m ~8,3 10-12 m. (A) Fusion nucléaire.   31H + 21H ---> 42He + 10n Analyse : énergie libérée. 31H 21H 42He énergie (MeV) de liaison par nucléon 2,8 1,2 7,1 énergie (MeV) 2,8*3 =8,4 1,2*2 = 2,4 7,1*4 =28,4 énergie libérée : 28,4-2,4-8,4 =17,6 MeV. (E)

c

retour -menu