loi de Boyle-Mariotte, diagramme d'Amagat concours physique ITPE 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Un liquide est réputé incompressible comparé à un gaz. En déduire lequel est le plus facile à faire monter à une pression de 100 bar. Dans tous les états de la matière, les mollécules sont attirées les unes vers les autres, et en même temps repoussées par les chocs dûs à leur agitation thermique. Les molécules s'entrechoquent constamment. Dans les gaz, elles sont très éloignées les unes des autres, et il n'est pas très difficile de les rapprocher en augmentant la pression. Dans les liquides, elles ont très proches les unes des autres. Leur proximité est si grande que des forces s'exercent pour repousser les molécules (force de Van der Waals). Alors il est très difficile de comprimer un liquide. Dans les solides, les molécules sont plus ou moins rangées en cristaux ou en verres, et il est très difficile de les comprimer davantage. Bien que ce soit encore possible, mais avec des pressions énormes, qui déforment les mailles cristallines. La pression de la mer varie avec la profondeur : p(0 m) = 1 bar ; p(5 m) = 1,5 bar : p(10 m) = 2 bar. Calculer la valeur numérique du gradient de pression. Dp/Dh = (2-1) / 10 = 0,1 bar m-1. Démontrer que cette valeur est compatible avec la loi fondamentale de l'hydrostatique appliquée à l'eau. dp = - reaug dz ; p-p0 = - reaug (z-z0) , l'indice zéro indique la surface du liquide ; l'axe z est vertical vers le haut p-p0 = -1000 *9,8 (z-z0) = -9,8 103(z-z0) A une profondeur de 10 m, (z-z0) = -10 d'où p-p0 =9,8 104 Pa ~ 1 bar. Lors du passage des niveaux de plongée, on demande aux postulants d'effectuer quelques calculs élémentaires en supposant toutes les transformations isothermes et les gaz parfaits. Un bloc est une bouteille de plongée de volume Vbloc =12 L. Un plongeur respire un air qui est obligatoirement à la pression de l'eau. Le volume d'air dans un poumon est d'environ 5 L. Un plongeur débutant peut voir le mauvais réflexe de retenir sa respiration sur les 5 derniers mètres de la remontée. Quel volume risque alors d'occuper l'air dans ces poumons ? Quantité de matière d'air et température sont constantes, donc Pini Vini = Pfin Vfin. Pini = 1,5 bar ; Vini = 5 L( à une profondeur de - 5 m ) ; Pfin = 1 bar ( en surface) Vfin = 1,5 *5 / 1 = 7,5 L, le volume des poumons serait devenu trop important par rapport au volume de la cage thoracique. Il faut donc expirer en remontant. Un plongeur plonge à 10 m. Son manomètre indique alors 200 bar. Il doit remonter avant que son manomètre indique 50 bar. Il ventile 20 L par minute. Combien de temps peut-il rester à cette profondeur ? Volume de la bouteille * pression initiale = 12 10-3 *200 105= 2,4 105 S.I. en supposant une température de 20 °C = 293 K et en prenant R = 8,3 J K-1mol-1, la quantité de matière initiale d'air est : ni =2,4 105 /(RT) =2,4 105 /(8,3*293) =98,7 moles. Volume de la bouteille * pression finale = 12 10-3 *50 105= 6 104 S.I. nf =6 104 /(RT) =6 104 /(8,3*293) =24,7 moles. variation : ni -nf =98,7-24,7 = 74 moles. Le plongeur respire de l'air à une pression de 2 bar = 2 105 Pa (pression à la profondeur de 10 m) Volume d'air disponible : 74*8,3*293 / 2 105 =0,9 m3 = 900 L. durée : 900/20 = 45 min. On souhaite remplir un bloc où la pression initiale est Pbloc = 1 bar. On utilise deux tampons ayant chacun un volume Vtampon =30 L et péalablement remplis d'air sous une pression de Ptampon = 220 bar. On branche le bloc sur le premier tampon ; on ouvre les vannes et les pressions s'égalisent à p1 dans le bloc et le premier tampon ; on ferme alors les vannes. Calculer p1. On écrit la conservation de matière d'air dans le bloc et le premier tampon. état initial : Pbloc Vbloc/ (RT) + PtamponVtampon /(RT) = (Pbloc Vbloc+PtamponVtampon )/(RT) état final : p1 (Vtampon +Vbloc)/ (RT). (Pbloc Vbloc+PtamponVtampon ) = p1 (Vtampon +Vbloc) ; p1 =(Pbloc Vbloc+PtamponVtampon ) / (Vtampon +Vbloc) p1 = (1*12+220*30) / (12+30) = 157 bar. 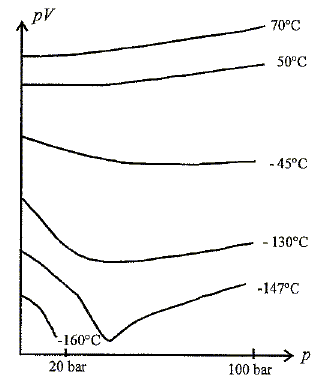On branche ensuite ce bloc sur ce second tampon et on effectue les mêmes opérations. les pressions s'égalisent alors à p2 dans le bloc et le second tampon. Calculer p2. On écrit la conservation de matière d'air dans le bloc et le second tampon. état initial : P1 Vbloc/ (RT) + PtamponVtampon /(RT) = (P1 Vbloc+PtamponVtampon )/(RT) état final : p2 (Vtampon +Vbloc)/ (RT). (P1 Vbloc+PtamponVtampon ) = p2 (Vtampon +Vbloc) ; p2 =(P1 Vbloc+PtamponVtampon ) / (Vtampon +Vbloc) p1 = (157*12+220*30) / (12+30) = 202 bar. Compression isotherme d'un gaz. Ci-dessous un diagramme d'Amagat ( pV fonction de p) avec les isothermes correspondant au gaz diazote. p est la pression, V est le volume. On constate qu'en dessous de -147°C, les courbes isothermes sont interrompues. A quel phénomène physique cela est-il dû ? Quel nom donne t-on à la température de -147°C pour l'azote ? Au-dessous d’une température (-147 °C pour le diazote) les courbes sont interrompues car le gaz se liquéfie. Cette température est appelée température critique et notée TC . Comment devraient être ces courbes dans le cas d'un comportement de gaz parfait ? gaz parfait : gaz constitué de particules suffisamment éloignées les unes des autres afin que leurs interactions soient très faibles, voir nulles. Dans ce cas, l’énergie potentielle d’interaction entre les molécules est négligeable devant l’énergie d’agitation thermique.( kT) Un gaz réel sous faible pression se comporte comme un gaz parfait. Dans l'hypothèse d'un gaz parfait, pV=cste, ces courbes devraient être des droites horizontales. Pourquoi n'observe t-on pas ce comportement sur ce diagramme ? Les gaz réels ne se comportent comme des gaz parfaits qu'aux faibles pressions et loin de leur température de liquéfaction.

retour -menu