Pendule électrostatique, énergie, concours physique ITPE 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

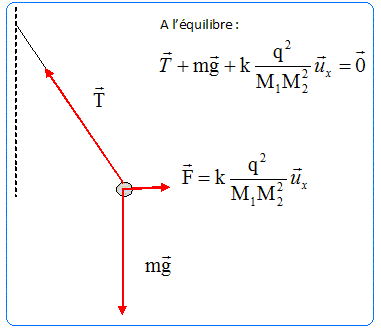
On considère le système représenté ci-dessous. Les deux points matériels M1 et M2 ont la même masse m et portent la même charge +q. Les deux fils de longueur L sont supposés inextensibles et sont attachés au même point O. On note a l'angle entre la verticale et le fil OM1. Représenter sur un schéma les forces appliquées à M1. Par projection de cette condition d'équilibre, déduire deux relations scalaires. 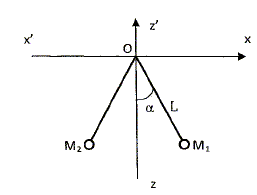M1M2 = 2Lsin a ; projection sur x'Ox : -T sin a + kq2 / (2Lsin a)2 = 0 projection sur z'Oz : T cos a -mg = 0. En travaillant dans l'approximation des petits angles, déterminer l'expression de a éq. On donne k = 9 109 SI. sin a~ a ; cos a~ 1 d'où T~ mg et mg a = kq2 / (2L a)2 ; a3 = kq2 / (4L2 mg) ; a =[ kq2 / (4L2 mg)]1/3. A.N : g = 10 m /s2 ; L = 1 m ; m = 10 g ; q = 3 10-7 C. a =[ 9 109 *(3 10-7)2 / (4*0,01*10)]1/3=0,126 rad ~ 0,13 rad. 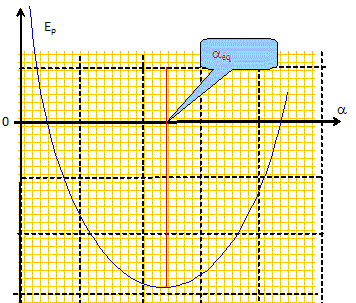Déterminer à une constante près, l'énergie potentielle de pesanteur du point matériel M1 : Epp = mgz + cste= -mgL cos a + cste. On peur choisir le point O comme origine de l'énergie potentielle de pesanteur ; dans ce cas la constante est nulle. Déterminer à une constante près, l'énergie potentielle d'interaction électrostatique du point matériel M1 : Epe = k q2/M1M2 + cste = k q2/(2Lsin a ) + cste. Commenter l'expression de l'énergie potentielle du système constitué par les deux charges : Ep = 2mgz + k q2/(x1-x2 ) + cste, où z est l'ordonnée commune des deux charges et x1, x2 sont les abscisses respectives de M1 et M2. Le premier terme est une fonction croissante de z ; le second terme est une fonction décroissante de (x1-x2 ) : la somme des deux termes prévoit l'existence d'un minimum de l'énergie potentielle. Par un développement limité à l'ordre 2 montrer que l'expression de l'énergie potentielle est : Ep(a) =-2mgL(1-a2/2) +kq2/(2La) Epp = -2mgL cos a. ( origine en O) avec cos a~ 1-½a2 si a est petit. Epe =k q2/(2Lsin a ). ( l'énergie potentielle électrostatique est nulle quand les charges sont suffisamment éloignées. avec sin a~ a si a est petit. d'où Ep ~k q2/(2L a ) - 2mgL( 1-½a2) A partir de l'expression de Ep retrouver l'expression de a éq. La position d'équilibre correspond à un extrémum de l'énergie potentielle. On cherche la valeur de a qui annule la dérivée de l'énergie potentielle. dEp/da = -k q2/(2L a2 ) + 2mgLa = 0 ; a =[ kq2 / (4L2 mg)]1/3. Tracer l'allure de Ep pour a petit. L'équilibre trouvé est-il stable où instable ? La position d'équilibre correspond à un minimum de l'énergie potentielle : l'équilibre est stable.

retour -menu