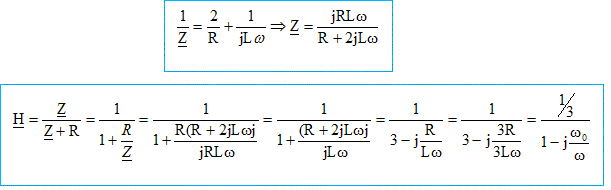Circuit RL: tensions continue et alternative, filtre, Bode En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

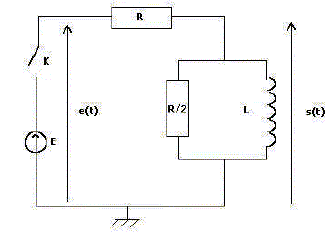
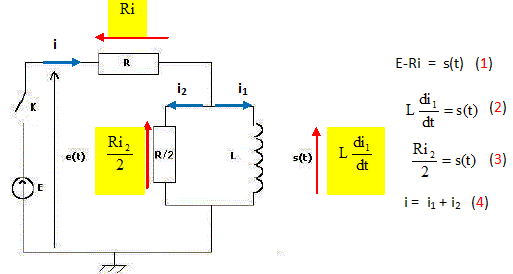
Le circuit ci-dessous est alimenté par un générateur de courant continu de fem E. A l'instant t=0, on ferme l'interrupteur K. Y a-t-il continuité de la tension s(t) à t=0 ? Y a-t-il continuité du courant dans la résistance R en t=0 ? Commenter physiquement les réponses. En déduire le comportement de s(t) au voisinage de t = 0+. Déterminer le comportement asymptotique de s(t) lorsque t tend vers l'infini. Peut-on à priori affirmer la continuité de certaines grandeurs électriques ( autres que celles étudiées ci-dessus ) en t=0 ? Justifier. La continuité de l'énergie électromagnétique ( ½Li12) dans la bobine, impose la continuité de l'intensité  i1 du courant dans la bobine. A t = 0-, les intensités i, i1 et i2 sont nulles. s(t=0-) = ½Ri2 = 0. A t = 0+, i1 = 0, la bobine introduit un retard à l'établissement du courant. (4) conduit à i = i2 ; soit s(t = 0+) = ½Ri Additivité des tensions E = Ri + s(t = 0+) = Ri+½Ri ; i(t = 0+) = 2E / (3R). Par suite s(t = 0+) = ½Ri(t = 0+) ; s(t = 0+) = E / 3. Il y a discontinuité de la tension s(t) à t=0. i2(t=0-) = i (t=0-) =0 ; i2(t=0+) = i (t=0+) = 2E / (3R). Il y a discontinuité des intensités des courants i et i2 à t=0. Quand le temps devient très grand, l'intensité du courant dans la bobine est constant ; sa dérivée par rapport au temps est nulle : d'après (2) s (t) tend vers 0 au bout d'un temps suffisamment long. Etablir l'équation différentielle vérifiée par s(t). En déduire s(t). Tracer l'allure de s(t). (1) et (3) donnent : E-Ri = ½R i2 ; i2 = 2E/R -2i repport dans (4) : i = i1 + 2E/R -2i ; 3 i = i1 + 2E/R ; différentier par rapport au temps : 3 di/dt = di1/dt ; tenir compte de (2) : 3L di/dt =s(t) Différentier (1) par rapport au temps : -Rdi/dt = ds(t) / dt soit : ds(t) dt + R 3L s(t) =0 On pose t = 3L/R, constante de temps. 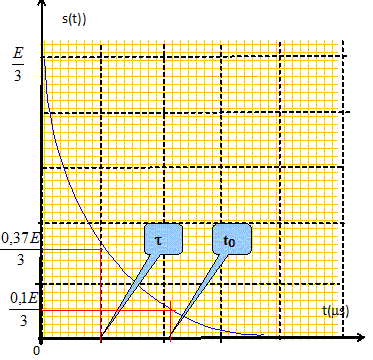La solution de l'équation différentielle est du type s(t) = A exp(-t/ t ) . La constante A est déterminée par les conditions initiales s(t=0+) = E/3. s(t) = E/3 exp(-t/ t ) . Exprimer en fonction de L et R le temps t0 au bout duquel s(t0) =0,1. s(t=0+). En déduire une méthode expérimentale pour déterminer t0 à l'oscilloscope. On précisera le montage électrique à réaliser et la mesure à effectuer concrètement.  0,1 E/3 = E/3 exp(-t0/t) ; ln 0,1 =-ln 10 = -t0/t ; t0 = t ln10 ; t0 = 3L ln10 /R. Brancher un oscilloscope à mémoire aux bornes de la bobine inductive. On mesure expérimentalement t0 = 3 microsecondes. On donne R= 1000 ohms. En déduire L. L = Rt0 3 ln 10 = 1000*3 10-6 3 ln 10 = 4,3 10-4 H On remplace le générateur continu par un générateur délivrant un signal périodique en créneaux. Quel doit être l'ordre de grandeur de la fréquence du générateur pour que l'on puisse effectivement mesurer t0, en utilisant la méthode indiquée, à l'oscilloscope ? La période du signal du GBF doit être un peu supérieure à t0 ; La fréquence doit donc être un peu inférieure à 1/t0. 1/310-6 ~3 105 Hz. 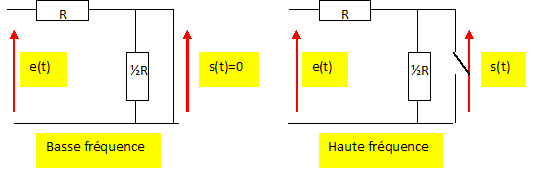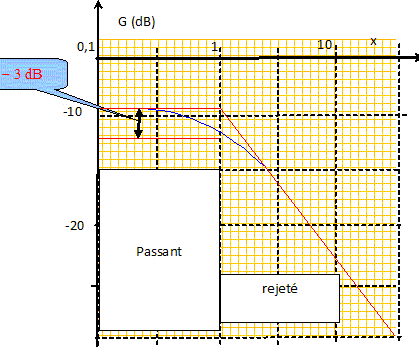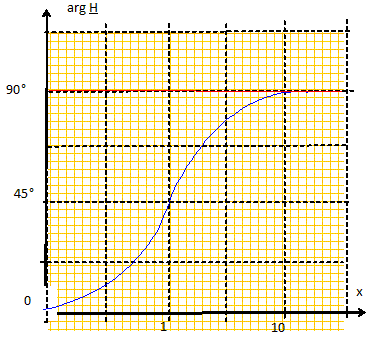Etude en régime sinusoïdal : On remplace le générateur précédent par un générateur sinusoïdal de féquence f et de tension efficace E, l'interrupteur étant fermé. On associe à la grandeur u(t) = U cos ( wt+j), la grandeur complexe u= U exp(j(wt+j)) avec w = 2pf. Comment se comporte le circuit en hautes et basses fréquences ? Quel est la nature du filtre que constitue le circuit ?   Filtre passe haut. Etablir la fonction de transfert en notation complexe H = s / e. Mettre le résultat sous la forme H0 / (1+f0/jf) Exprimer H0 et f0 en fonction de L et R. On note Z l'impédance complexe de la portion de circuit ½R et L en dérivation. H0 = 1/3 et w0 = R/(3L) et w = 2pf. En déduire la fréquence de coupure du filtre à - 3 dB, qu'on notera fc. Comment se détermine t-elle expérimentalement ? Le module de H est noté H ; le gain en décibel vaut : G = 20 log H. On pose : x = w0 / w. H = 1 3 1+jx 1+x2 H= 1 3 (1+x2)-½ G = 20 log (1/3) - 10 log ( 1+x2) = -9,5 - 10 log ( 1+x2). si x<<1, G ~ -9,5 dB droite horizontale asymptote si x>>1, G= -9,5 -20 log x ( droite asymptote de pente -20 dB par décade ). Fréquence de coupure à -3 dB. -12,5 = -9,5 - 10 log ( 1+x2) ; 0,3 =log ( 1+x2) 2 = 1+x2 ; x = 1 ; or x = w0 / w ; wc = w0 = R/(3L). Tracer l'allure du diagramme donnant le module de H et l'argument de H en fonction de la fréquence f.  L'argument de H vaut : arg H= tan-1 x. si x<<1, arg H =0 : droite horizontale asymptote si x>>1, arg H =90 : droite horizontale asymptote.

retour -menu