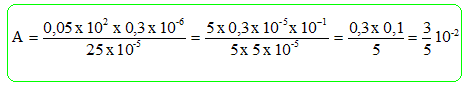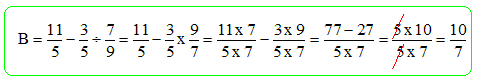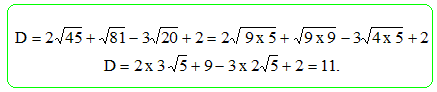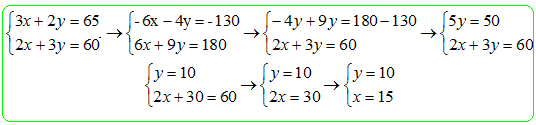Mathématiques : concours ASPTS agent spécialiste police technique et scientifique ; Lyon 2007. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Indiquer la bonne réponse. L'expression A est égale à : 3 10-2 ; -3 10-2 ; 3 / 5 10-2. L'expression B est égale à :10 / 7 ; -3 / 7 ; 1/ 7. 4 (x-3) - 3 (1 /3 -2x) = 13(x-1) a pour solution : -3 ; 0 ; 3 4x -12 -1 +6x = 13 x -13 10x -13 = 13x -13 ; 13 x -10x = 13-13 ; 3 x=0 ; x =0. L'expression C est égale à : 16 ; 8 - 2 racine carre (5) ; 11. L'expression D est égale à : 11 ; 5 - 5 ; 3 -2 ; 5 Résoudre le système d'équations suivant par combinaison : Un torréfacteur met en vente 2 sortes de mélange de café. Le mélange A est composé de 60 % d'Arabica et de 40 % de Robusta et coûte 13 € le kilogramme. Le mélange B est composé de 40 % d'Arabica et de 60 % de Robusta et coûte 12 € le kilogramme.On appellera X le prix du kilogramma d'Arabica et Y le prix du kilogramme de Robusta. Quel est le prix du kilogramme d'Arabica et du kilogramme de Robustat ? 0,6 X + 0,4 Y = 13 (1) et 0,4 X +0,6 Y = 12 (2) Multiplier tout par 5 afin de retrouver le système ci-dessus. 3X +2Y = 65 et 2X +3Y = 60. 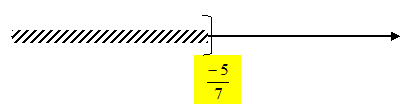(X = 15 et Y = 10 ) On donne l'expression suivante C = (3x-2)2-25 Développer et réduire C. C = 9x2-12x+4-25 ; C =9x2-12x-21. Factoriser C. Différence de deux carrés A2-B2 = (A-B)(A+B) avec A = 3x-2 et B =5. C = (3x-2-5)(3x-2+5) =(3x-7)(3x+3) = 3(3x-7)(x+1). Calculer C pour X = 1/3. (3x-2)2 = (1-2)2 = 1 ; C =1-25 = -24. Résoudre (3x-7)(x+1) =0. 3x-7 = 0 ; 3x = 7 ; x = 7/3. et x+1=0 ; x = -1. Résoudre l'inéquation 4x+7 >2-3x et représenter ses solutions sur une droite graduée. 4x +3x >2-7 ; 7x >-5 ; x >-5/7.   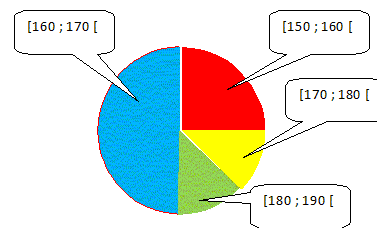Le tableau ci-dessous indique la répartition des élèves d'une classe suivant leur taille. Compléter le tableau : tranche de taille taille en cm effectif ni ( nombre d'élèves) fréquence fi en % effectifs cumulés croissants en % effectifs cumulés décroissants en % angles en ° A [150 ; 160 [ 8 25 25 100 90 B [160 ; 170 [ 16 50 75 25 180 C [170 ; 180 [ 4 12,5 87,5 12,5 45 D [180 ; 190 [ 4 12,5 100 0 45 Total xxxxxxxxxxxxx 100 xxxxxxxxxxxxxx xxxxxxxxxxxxxx 360 Déterminer le nombre d'élèves mesurant moins de 170 cm. Taille inférieure à 170 cm ; 16 + 8 = 24. Déterminer le nombre d'élèves mesurant au moins de 170 cm. Taille supérieure à 170 cm ; 4 +4 = 8. Reproduire sur un diagramme circulaire, les différentes tranches de tailles des élèves.     Le prix officiel du véhicule Xsara Picasso est de 20 000 € H.T. Sachant que le taux de TVA appliqué est de 19,6 %, quel est le prix d'un tel véhicule TTC ? 20 000 *1,196 = 23 920 €. On a relevé les notes obtenues par de élèves à un devoir de mathématiques. notes 7 8 8,5 9 10 11 13 15,5 18 effectifs 1 2 2 4 4 6 2 2 2 Calculer la moyenne en détaillant les calculs. Effectif total : 1 +2 +2 +4 +4 +6 +2 +2 +2 = 25. moyenne : (7 +8*2 +8,5*2 +9*4 +10*4 +11*6 +13*2 +15.5*2 +18*2) / 25 (7 +16 +17 +36 +40 +66 +26 +31 +36) / 25 = 11. Déterminer la médiane en justifiant. La médiane est  le nombre qui permet de couper la population étudiée en deux groupes contenant le même nombre d'individus L'un des groupe a des notes supérieures à la note médiane, l'autre groupe a des notes inférieures à la note médiane.   notes 7 8 8,5 9 10 11 13 15,5 18 effectifs 1 2 2 4 4 6 2 2 2 effectif cumulé croissant 1 3 5 9 13 19 21 23 25 (25 +1) / 2 = 13 ; la note médiane est la 13è note, c'est  à dire 10. Mika propose des boules de glace de 2 cm de rayon. Calculer le volume d'une boule en fonction de pi. 4 /3 pi R3 = 4/3 pi *23 =10,67 pi cm3. Des clients très gourmands ont réclamé des boules plus grosses. Mika a doublé le rayon de ces boules. Par combien le volume d'une boule a t-il été multiplié ? Le volume est proportionnel au cube du rayon ; si le rayon double, le volume est multiplié par 23=8.

retour -menu