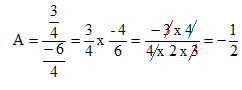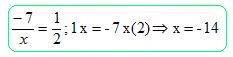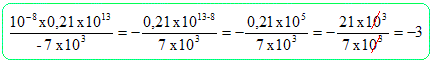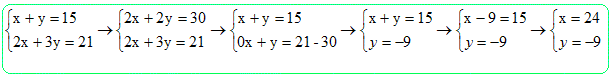Mathématiques : concours ASPTS agent spécialiste police technique et scientifique ; Lyon 2006. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Choisir la bonne réponse. L'expression A est égale à : 1 / 2 ; -18 / 12 ; -1 / 2. L'équation suivante a pour solution : -7 / 2 ; -14 ; -2 / 7. L'expression suivante est égale à : -3 ; 3 ; -1/3. L'équation : 3(x-2) -(x+2) = 2x-8 a pour solution : 0 ; 8 ; -4. 3x - 6 - x -2 = 2x - 8 2x - 8 = 2 x -8 Cette égalité est toujours vérifiée quelle que soit la valeur donnée à x. L'expression suivante est égale à : 1,2 ; -1 / 12 ; -13 / 12. Un bassin est alimenté par deux fontaines dont le débit est constant. Si on laisse couler la première fontaine pendant 4 heures et la seconde pendant 3 heures, la quantité d'eau recueillie au total est 55 L. Si on laisse couler la première fontaine pendant 3 heures et la seconde pendant 4 heures, la quantité d'eau recueillie au total est 57 L. Calculer en L / h le débit de chaque fontaine. On note x le débit de la fontaine n°1 et y le débit de la seconde fontaine. 4 x + 3 y = 55 (1) ; 3x + 4 y = 57 (2) On multiplie (1) par 3 et (2) par 4 puis on soustrait : 12 x + 9 y = 165 et 12x + 16 y = 228 (2) 12 x - 12 x +16y - 9y = 228 -165 ; 7 y = 63 ; y = 63 / 7= 9. par suite (1) donne : 4 x +3 x 9 = 55 ; 4x = 55-27 ; 4x =28 ; x = 7. Fontaine n°1 : 7 L/h ; fontaine n°2 : 9 L/h. Résoudre le système suivant :       Le granite est une roche cristalline formée d'un mélange hétérogène de 4 éléments : quartz, feldspath, biotite et minéraux secondaires. Un bloc de granit est constitué de : 28 % de quartz, 53 % de feldspath, 11 % de biotite et 19,2 dm3 de minéraux secondaires. Calculer le volume de ce bloc. Pourcentage de minéraux secondaires : 100 - (28 +53 +11) = 8 % 0,08 ( 8 %) correspond à 19,2 dm3 1 ( 100 %) correspond à : 19,2 / 0,08 =240 dm3. 1 m3 de ce granite a une masse de 2,6 tonnes. Calculer la masse de ce bloc de granite. 240 dm3 = 0,24 m3. puis 0,24 * 2,6 = 0,624 tonne. Soit A = (x-2)2-16. Développer et réduire A. A = x2-4x +4-16 = x2-4x -12. Factoriser A. Différence de deux carrés : X2-Y2 = (X+Y) ( X-Y) avec X = x-2 et Y = 4 A = (x-2+4)(x-2-4) = (x+2) ( x-6). Résoudre l'équation (x-2)(x+6)=0. x+6 = 0 soit x = -6 et x-2 = 0 soit x = 2.   Compléter le tableau suivant : Répartition des déchets ménagers pour une commune de 200 habitants. types de déchets nombre de tonnes fréquence (%) résidus alimentaires 155 155/700*100 =22,14 papiers, cartons 210 210 / 7 = 30 verres 70 70 / 7 =10 plastiques 55 55 / 7 =7,86 métaux 30 30 / 7 =4,29 divers 180 180 / 7 =25,7 total 700 100 Le tableau ci-dessous donne la répartition des élèves d'une école suivant leur taille en cm. Calculer les fréquences correspondantes à chaque catégorie. taille (cm) [100 ; 110[ [110 ; 120[ [120 ; 130[ [130 ; 140[ [140 ; 150[ total effectifs 24 38 70 54 14 200 fréquence (%) 24/2 =12 38/2 =19 70/2=35 54/2=27 14/2=7 100 Combien d'élèves mesurent au moins 120 cm ? La taille doit être supérieure ou égale à 120 cm : 70+54+14 =138. Combien d'élèves mesurent moins de 140 cm ? Seuls 14 élèves ont une taille supérieure ou égale à 140 cm : 200-14 =186. Combien d'élèves mesurent entre 110 et 140 cm ? 38+70+54=162. Tracer l'histogramme de cette série.

retour -menu