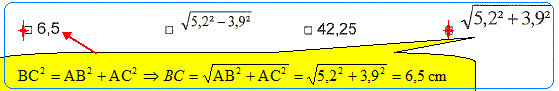Mathématiques : concours ASPTS agent spécialiste police technique et scientifique ; Sud-Ouest 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

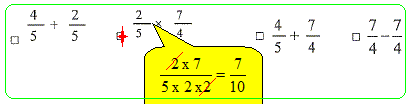
Indiquer la ou les bonne réponses. Soit l'expression A = Pour commencer le calcul de A, on peut commencer par : La multiplication est prioritaire sur l'addition et sur la soustraction. La valeur de A est égale à : L'écriture scientifique du nombre 20,52 est : 2,052 10-1 ; 0,2052 102 ; 2,052 101 ; 2052 102. Pour effectuer un réglage rapide des feux de croisement d'un véhicule, on place celui-ci devant un mur vertical comme l'indique le schéma suivant : Sachant que la portée des feux de croisement est HM = 30 m, la portée des feux est HP = 0,8 m, la distance entre le mur et la voiture est AH = 3 m : Calculer la distance AM et la hauteur de réglage AB. AM = HM - AH = 30 - 3 = 27 m. HM HP AM x HP 27 x 0,8 = ; AB = = = 0,72 m AM AB HM 30 Soit un triangle rectangle ABC rectangle en A. On donne AB = 3,9 cm et AC = 5,2 cm. Pour calculer la longueur CB, on utilise : - le théorème de Thalès - la réciproque du théorème de Pythagore - le théorème de Pythagore - un autre théorème. La longueur BC est alors égale à : Deux amis ont ensemble une somme de 85 euros, l'un possède 7 euros de plus que l'autre. Calculer se que possède chaque ami. On note x et y les sommes possédées : x + y = 85 (1) x = y+7 ; repport dans (1) ; y+7 + y = 85 ; 2 y = 85-7 ; 2y = 78 ; y = 78 / 2 = 39. d'où x = y+7 = 39+7 = 46 euros. Lorsqu'on triple la longueur des arètes d'un cube, on multiplie le volume du cube par : 3 ; 9 ; 18 ; 27. Volume du cube = arète 3 ; en multipliant l'érète par trois, le volume du cube est multiplié par 33 = 27. Parmi les inéquations proposées, quelles sont celles qui sont fausses ? 6,03 < 6,3 ( vrai) ; -4,3 > -4,03 ( faux ) ; 8,2 10-3 > 0,082 ( faux ) : [ 0,082 = 82 10-3 ] ; -0,0151 < -0,015 ( vrai). Sur le marché, des agriculteurs ont procédé aux échanges suivants : - 12 lièvres contre 5 dindons ; 5 poulets contre 2 canards ; 7 dindons contre 8 oies ; 10 canards contre 3 lièvres Sachant qu'une oie vaut 52,5 euros, quel est le prix d'un poulet ? 2,5 ; 3 ; 3,5 ; 4 euros. "7 dindons contre 8 oies " : prix d'un dindon = 8*52,5 / 7 = 60 euros. "12 lièvres contre 5 dindons" : prix d'un lièvre = 5*60 / 12 = 25 euros " 10 canards contre 3 lièvres" : prix d'un canard = 3*25/10 = 7,5 euros " 5 poulets contre 2 canards" : prix d'un poulet : 2*7,5 / 5 = 3 euros. Au terme d'une année, un épargnant qui a placé 10 000 euros en actions voit son capital progressé de 25 %. L'année suivante ses actions retrouvent la valeur de 10 000 euros. Quel est le pourcentage de baisse enregistré la deuxième année ? Valeur des actions au bout d'un an : 10 000*1,25 = 12500 euros. Baisse au cours de la deuxième année : 2500 euros soit 2500 *100 / 12500 = 20 %.     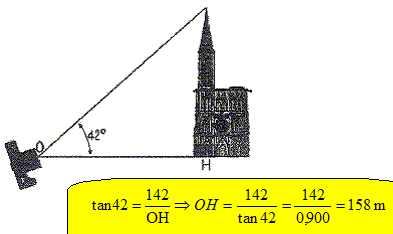La catédrale de Strasbourg mesure 142 m de haut. L'appareil photo est muni d'un objectif dont dont l'angle d'ouverture est 42 °. Calculer la distance minimale OH pour que la cathédrale apparaisse entièrement dans l'objectif.  Le nombre 3 x 10-3 x 0,2 x 102 peut s'écrire : 0,6 10-1 ; 0,6 10-6 ; 0,06 ; 0,05. 3 x 0,2 x 10-3 x 102 = 0,6 x 10-1 = 0,06. Un client achète dans un supermarché 5 bouteilles de jus d'orange et 3 bouteilles de pomme pour 16,4 euros. Le jour suivant il rachète 3 bouteilles de jus d'orange et 5 bouteilles de jus de pomme pour 15,6 euros. Quel est le prix d'une bouteille de jus d'orange ? On note x le prix d'une bouteille de jus de pomme et y le prix d'une bouteille de jus d'orange. 5 y + 3 x = 16,4 (1) ; 3y + 5x = 15,6 (2) Multiplier (1) par 5 et (2) par 3 puis soustraire : 25 y + 15 x = 82 ; 9y + 15x = 46,8 25y-9y = 82 -46,8 ; 16 y =35,2 ; y = 35,2 / 16 ; y = 2,2 euros. Pour construire un garage, il faut trois maçons pendant 16 jours. Combien de temps faudrait-il avec 4 maçons ? ( 15 ; 14 ; 13 ; 12 jours ) 3 x 16 / 4 = 12 jours.   Un même produit est vendu sous différentes formules : - un paquet de 200 g à 15 euros - un paquet de 250 g à 19 euros - un lot de deux paquets de 50 g pour 8 euros - un lot de trois paquets de 100 g plus un paquet de 25 g pour 25 euros. Quel est le plus économique ? "un paquet de 200 g à 15 euros" soit 15 x1000 / 200 = 75 euros le kg "un paquet de 250 g à 19 euros" soit 19 x1000 / 250 = 76 euros le kg " un lot de deux paquets de 50 g pour 8 euros" soit 8 x 1000 / 100 = 80 euros le kg "un lot de trois paquets de 100 g plus un paquet de 25 g pour 25 euros" soit 25 x 1000 / 325 = 76,9 euros le kg. Une boîte sans couvercle a la forme d'un cube de 6 cm de côté. Elle est faite d'un bois dont une plaque de 10 cm sur 10 cm pèse 50 g. Quelle est sa masse ? ( 108 g ; 90 g ; 300 g ; 360 g ) La boîte possède 4 côtés et un fond, soit 5 carrés de surface totale : 5 x 6 x 6 = 180 cm2. Masse d'une plaque carrée de 10 cm sur 10 cm ( surface 100 cm2) : 50 g. Masse de la boîte : 50 x 180 / 100 = 90 g. Dans une entreprise on a recensé l'âge du personnel. On a ainsi rempli le tableau suivant : âge ( années) 25 30 40 50 60 nombre de personnes 6 15 5 10 4 Calculer l'âge moyen du service. Nombre total de personnes :N = 6+15+5+10+4 = 40 25 x 6 + 30 x 15 + 40 x 5 + 50 x 10 +60 x 4 = 150 + 450 + 200 + 500 + 240 =1540 puis diviser 1540 par 40 : 1540 / 40 = 38,5 ans. Le développement de l'expression (x-3) ( x-2 ) est égale à : x2-3x-2x-6 ; x2-2x-3x+6 ; -4x2+6 ; -5x + x2 + 6. (x-3) ( x-2 ) = x2 -2x -3x +6 = x2 -5x +6. Un automobiliste relie deux villes en 3 h 45. Il roule à 20 m / s pendant les 2 / 5 ème du trajet, puis il augmente sa vitesse de 50 % pendant le tiers suivant et termine son parcours à 60 km / h. Quelle distance en km sépare les deux villes ? On note d la distance séparant les deux villes. 3 h 45 min = 3 h + 0,75 h = 3,75 heures. Durée de la première partie : 3,75 x 2 / 5 = 1,5 heures ou 90 min ou 5400 s. Distance parcourue : 5400*20 = 108 000 m = 108 km. Durée de la seconde partie : 3,75 x 1 / 3 = 1,25 heures ou 75 min ou 4500 s. Vitesse : 20*1,5 = 30 m/s ; distance parcourue : 30*4500 = 135 000 m = 135 km. Durée de la troisième partie : 3,75 - 1,5-1,25 = 1 heure Distance parcourue : 60 km. 108+135+60 = 303 km.

retour -menu