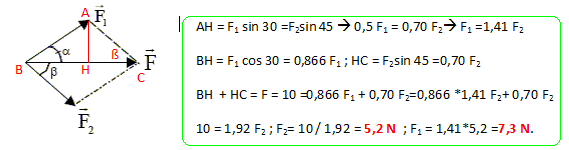QCM mécanique : cinématique ( 12 questions) : concours kiné Poitiers 1999. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

On donne c = 3 108 m/s ; distance Terre-Soleil ~ 150 106 km. Quelle proposition est vraie ? - la vitesse du son dans l'air à 25°C est 340 km/s ( 340 m/s) - la masse d'un électron est environ 10-40 kg ( 10-30 kg) - le rayon de la Terre est de l'ordre de 4 1010 mm (4 1010 mm = 4 107 m =4 104 km : le rayon de la Terre est de l'ordre de 6400 km ) - il faut environ 8 min à la lumière émise par le soleil pour parvenir à la Terre ( 150 109 / 3 108 = 500 s ~8,3 min) Vrai. - l'accélération de la pesanteur sur la Lune est 60 fois plus faible que sur la Terre ( 6 fois plus faible que sur Terre). Un vase calorimétrique, très bien isolé contient de l'eau à 30 °C. La capacité thermique de l'ensemble ( eau + vase ) est 1250 J K-1. On introduit dans ce calorimètre 120 g de glace à -20 °C. La capacité thermique massique de la glace est 2100 J kg-1 K-1. La chaleur latente de fusion de la glace est 335 kJ kg-1. Lorsque l'équilibre thermique est atteint, le calorimètre contient : - uniquement de la glace à une température inférieure à 0°C - un mélange eau + glace à 0°C - uniquement de la glace à 0°C - uniquement de l'eau liquide à 0°C - uniquement de l'eau liquide à une température supérieure à 0°C. On note qéq la température d'équilibre. Hypothèse n°1 : qéq = 0°C. Energie perdue par les corps chauds ( calorimètre + eau) : 1250*(0-30) =37 500 J. Energie gagnée par le corps froid, la glace : -pour se réchauffer de -20 °C à 0°C : 2100 * 0,120*(0-(-20)) = 5040 J. por fondre à 0°C : 0,12*335 103 =40 200 J Total : 40 200 + 5040 = 45 240 J. Cette valeur étant supérieure à l'énergie cédée par les corps chauds, toute la glace ne peut pas fondre. Les coordonnées du vecteur position et du vecteur vitesse d'un mobile ponctuel aux dates t1 = 2s, t2 =4 s et t3 = 5 s sont les suivantes : date t(s) position (m) vitesse (m s-1) 2 x=4 x'=4 y=8 y'=8 z=0 z'=0 4 x=16 x'=8 y=32 y'=16 z=0 z'=0 5 x=25 x'=10 y=50 y'=20 z=0 z'=0 A la date t=0, x0=y0=z0=0. Ces données sont compatibles avec certaines des hypothèses suivantes, précisez lesquelles : - le mouvement est plan ( z = 0 et z' =0 aux trois dates ) Vrai - le mouvement est rectiligne ( quand x est multiplié par 4, y est multiplié par 4 ; quand x est multiplié par 5, y est multiplié par 5 ) Vrai - le mouvement est uniforme ( uniforme signifie : la norme de la vitesse est constante ) - les coordonnées de l'accélération sont ax=2 m s-2 ; ay =2 m s-2 ; az = 0. (Dx'/Dt = (8-4) / 2 = 2 ou (10-4) / 3 = 2 ; Dy'/Dt = (16-8) / 2 = 4 ou (20-8) / 3 = 4 ) - à la date t=0 les composantes de la vitesses sont nulles.Vrai x'(2) = ax t+ x'0 ; 4 = 2*2 +x'0 d'où x'0 =0 y'(2) = ay t+ y'0 ; 8 = 4*2 +y'0 d'oùy'0 =0 Un mobile ponctuel M se déplace dans un plan muni d'un repère d'espace orthonormé ( O, i, j) (Les vecteurs sont écrits en gras et en bleu) A chaque instant t OM = (t+2) i + (3t2+5t) j. Ces données sont compatibles avec certaines des hypothèses suivantes, précisez lesquelles : - le mobile a un mouvement rectiligne et uniformément varié x = t+ 2 soit t = x-2 ; y = 3t2+5t = 3( x-2)2 + 5(x-2) y = 3x2-12x +12+5x-10 ; y = 3x2-7x +2 ( parabole) - le mobile a une trajectoire parabolique ( Vrai) - le vecteur vitesse du mobile est constant ( v =dOM /dt = 2 i + (6t+5) j ) - le vecteur accélération du mobile est constant ( a =dv /dt = 0 i + 6 j ) ( Vrai) - à l'instant t=0, initial, le vecteur vitesse est : v0 = i. ( v =dOM /dt = 2 i + (6t+5) j ; v0 = 2 i +5 j ) On décompose une force F en deux composantes F1 et F2 . a =30 ° ; ß = 45° ; norme de F = 10 N.   Dans ces conditions, les intensités F1 et F2 des forces sont : F1 = F2 = 5 N ; F1 =8,3 N, F2 = 6,2 N ; F1 =7,3 N, F2 = 5,2 N ; F1 =7,3 N, F2 = 8,3 N ; F1 =8,3 N, F2 = 5,2 N.       Dans le référentiel géocentrique supposé galiléen, un satellite de la terre décrit une orbite circulaire de rayon R. - la norme de sa vitesse est constante ( Vrai ) - son accélération est nulle ( aN = v2/R) - sa période de révolution est proportionnelle au rayon ( 3è loi de Kepler T2 = constante fois R3 ) - si le satellite est géostationnaire, sa vitesse est nulle - on pourrait placer un satellite de vitesse différente sur la même orbite. La période de rotation de la Terre dans un référentiel géocentrique vaut 86164 s. La Terre est supposée sphérique et de rayon R = 6370 km. L'accélération d'un point de la Terre de latitude 45° vaut : 2,39 10-2 m s-2 ; 3,38 10-2 m s-2 ; 1,69 10-2 m s-2 ; 2,39 cm s-2 ; 3,38 cm s-2 ; L'intensité de la force gravitationnelle exercée par la Terre sur la Lune vaut 1,98 1026 N. La masse de la Terre vaut environ 80 fois la masse de la Lune. Le rayon terrestre est 3,66 fois celui de la Lune. L'intensité de la force gravitationnelle exercée par la Lune sur la Terre vaut donc : 1,84 1023 N ; 2,48 1024 N ; 1,48 1025 N ; 5,41 1025 N ; 1,98 1026 N. La force attractive exercé par la Terre sur la Lune a même valeur que la force attractive exercée par la Lune sur la Terre.      Un automobiliste parcourt 400 m en 16,8 s, départ arrêté. Son accélération supposée constante vaut : 2,8 m s-2 ; 1,4 m s-2 ; 23,8 m s-2 ;25 m s-2 ; 12 m s-2 . Le mouvement est rectiligne uniformément accéléré : x = ½a t2 ; a = 2x / t2 =800 / 16,82 = 2,8 m s-2. Un solide de masse M inconnue est immobile sur un banc à coussin d'air horizontal. Lorsqu'on le soumet à une force constante F parallèle au ban, il parcourt une distance d =4 m en une durée t = 17,5 s. Un second solide, de masse M' =25 kg, est placé dans les mêmes conditions. Soumis à la même force il parcourt une distance d'=3 m en une durée t' = 27,6 s. Calculer la valeur de M. ( 2,21 kg ; 7,54 kg ; 1,32 kg ; 4,31 kg ; 1,52 kg. Sur la table à coussin d'air, le poids est compensé par l'action du support. La seconde loi de Newton s'écrit : pour le premier solide : F = Ma ; pour le second solide : F = M' a'. a = 2d / t2 = 8/17,52 =0,0261 m s-2 ; a' = 2d' / t'2 = 6/27,62 =7,876 10-3 m s-2 ; M = M' a' / a = 25*7,876 10-3 / 0,0261 =7,54 kg. Un pendule est constitué d'une petite bille assimilable à un point matériel de masse m = 200 g, reliée à un point O fixe par un fil inextensible de masse négligeable et de longueur L = 30 cm. Le pendule abandonné sans vitesse initiale avec un angle a0 = 30 °, oscille dans un plan vertical passant par le point O. Quel est l'angle entre le fil et la verticale quand la vitesse angulaire vaut 2,8 rad/s ? ( 0,18 rad ; 0,67 rad ; 2,42 rad ; 9,6 rad ; 10,4 rad ) 30° ~ 0,52 rad : l'angle ne peut pas dépasser 0,52 rad. Un mobile est animé d'un mouvement rectiligne sinusoïdal d'amplitude a = 24 cm et de période T = 4 s. On choisit comme origine des dates un instant d'élongation maximale positive. L'équation horaire du mouvement est, si l'amplitude est en mètre et le temps en secondes : x = 0,24 sin (½pi t ) ; x = 0,24 cos (½pi t ). x est de la forme x = 0,24 cos (wt+j) avec w = 2 pi /T = =2 pi / 4 = ½ pi. 0 l'instant initial, x = 0,24 m d'où : 0,24 = 0,24 cos j ; 1 = cos j ; soit j = 0. A l'instant t = 0,5 s, la vitesse du mobile est : 0 m s-1 ; -0,27 m s-1 ; +0,27 m s-1. v = dx /dt = -0,24 * 0,5 * pi sin (½ pi. t) = -0,377 sin(½ pi. t) v(t=0,5) = -0,377 sin (0,5*3,14 *0,5) = -0,377 sin (0,785) = -0,377 *0,707 = -0,27 m s-1.

retour -menu