|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
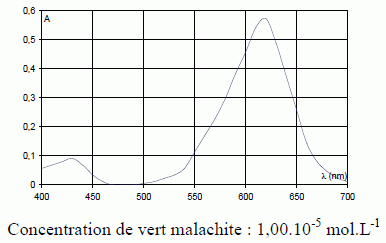
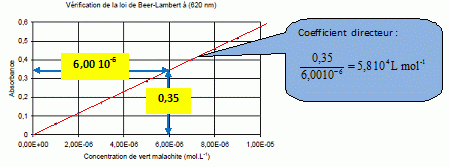
Le vert malachite (M+ + Cl-) représenté ci-dessous – ou violet d’aniline – a été utilisé pour traiter les infections fongiques et bactériennes dans le poisson et les oeufs de poisson. En milieu basique, les ions hydroxyde OH- peuvent se fixer sur le carbocation M+ , entraînant la décoloration de la solution suivant une réaction supposée totale : M+ + OH- → MOH. 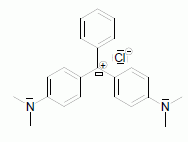 Enoncer la loi de Beer-Lambert, en nommant les paramètres qui y apparaissent et en spécifiant pour chacun d’eux une unité. La loi de Berr-Lambert exprime la variation de l'intensité lumineuse en fonction de la distance parcourue dans un milieu transparent. Lorsqu'une lumière monochromatique d'intensité I0 traverse un milieu homogène, l'intensité de la lumière émergente I décroît exponentiellement lorsque l'épaisseur l du milieu absorbant augmente. I = I0 . e (- al) a est une constante appelée coefficient d'absorption, caractéristique du milieu et de la longueur d'onde considérés. Dans le cas des solutions, la loi de Beer fait intervenir les concentrations. I = I0 . e (- elc) où e est un coefficient caractéristique de la substance appelé coefficient d'absorbance (L mol-1 cm-1), l est l'épaisseur de la cuve (cm) et c la concentration de la solution (mol/L). Cette loi est vérifiée lorsque la solution est de concentration inférieure à : c < 0,1 mol.L-1. La relation fondamentale utilisée en spectrophotométrie est présentée sous la forme : A= log (I0/I) = elc ( A est l'absorbance ou densité optique) e est une caractéristique de la molécule. Plus e sera grand, plus la solution absorbe. Nommer la courbe représentative de l’absorbance A en fonction de la longueur d’onde λ. Rappeler pourquoi on choisit en général la longueur d’onde pour laquelle l’absorbance est maximale lorsque l’on cherche à vérifier la loi de Beer-Lambert.
La courbe obtenue
étant une droite, la loi de Berr Lambert est vérifiée. Détermination
de la loi de vitesse. Proposer une expression de la loi de vitesse, en
notant k la constante de vitesse.
Montrer que la courbe ci-dessous permet de vérifier que β = 1 et de trouver la valeur de kapp. 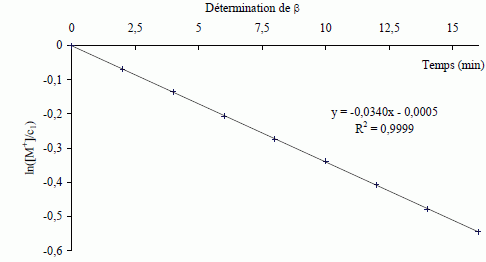 v = -d[M+]/dt = kapp[M+] ; d[M+] / [M+]ß = -kapp dt Hypothèse ß = 1 ; intégrer entre 0 et t : ln ([M+] / c1) = -kapp t. Si on trace la courbe d'équation ln ([M+] / c1) en fonction du temps, on obtient une droite de coefficient directeur -kapp. Le graphe ci-dessus étant une droite, l'hypothèse est bien vérifiée. kapp = 0,0340 min-1. De nouvelles expériences sont réalisées, en faisant varier la concentration c2 en ions hydroxyde.
Montrer que la courbe ci-dessous permet de trouver les valeurs de α et de k. Indiquer les résultats obtenus en précisant les unités. 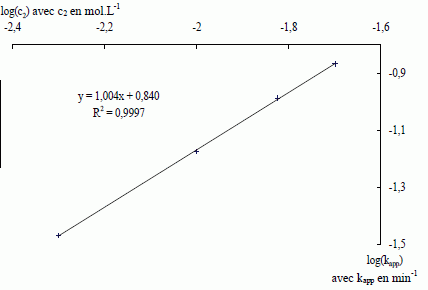 kapp = k [HO-]a ; ln kapp = a ln [HO-] +ln k = a ln c2 + ln k. La courbe d'équation ln kapp =f(ln c2) est une droite de pente a = 1,00. ln k = 1,92 ( voir 4è ligne du tableau ci-dessus) ; k = 6,82 L mol-1 min-1. Suivi cinétique
de la décoloration de la phénolphtaléine en milieu basique.
Montrer,
compte tenu des conditions initiales, que l’on peut se ramener à une
forme simplifiée pour la vitesse de la réaction se déroulant dans le
sens direct. On posera k1'=k1C0.
Etablir l’équation différentielle régissant l’évolution de x au cours du temps. On notera k = k'1 + k-1.
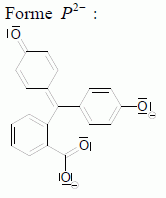
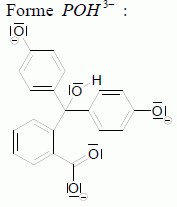
dx/dt = k'1 (C1 -x) + k-1 x = k'1 C1 - (k'1 + k-1) x = k'1 C1 -k x dx/dt + k x = k'1 C1. Résoudre cette équation différentielle et montrer que x = x∞(1 – exp(-kt)) Solution de l'équation sans second membre : x = A exp(-kt) avec A une constante. Solution particulière de l'équation complète : x = x∞ ( à l'équilibre) Solution générale de l'équation complète : x = A exp(-kt) + x∞ . On détermine A par la condition initiale x(t=0) = 0 : 0 = A + + x∞ ; A = - x∞. x = x∞(1 – exp(-kt)). La cinétique est suivie par spectrophotométrie. Dans les conditions choisies (λ =550 nm), seule la forme basique P2- de la phénolphtaléine absorbe.
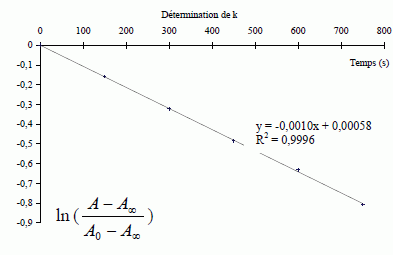
Montrer que : ln [(A-A∞) / (A0 -A∞) ] =-kt. [P2-] =C1 -x ; x =C1 -[P2-] ; x∞ = C1 - [P2-]∞ et x = x∞ (1– exp(-kt)) ; ( C1 -[P2-] ) = (C1 - [P2-]∞ ) (1– exp(-kt)) ; ( C1 -[P2-] ) / (C1 - [P2-]∞ ) =1– exp(-kt) ; 1- ( C1 -[P2-] ) / (C1 - [P2-]∞ ) = exp(-kt) ; ([P2-]- [P2-]∞ ) / (C1 - [P2-]∞ ) = exp(-kt) ; De plus absorbance A et concentration [P2-] sont proportionnelles, d'où : [(A-A∞) / (A0 -A∞) ] = exp(-kt) ; puis prendre le logarithme de chaque membre: ln [(A-A∞) / (A0 -A∞) ] =-kt.
On dispose d’une solution constituée d’un mélange : • d’acide sulfurique H2SO4 de concentration CA (1ère acidité forte ; pKa ( HSO4- / SO42-) = 2,0) ; • de chlorure d’ammonium (NH4+ + Cl-) de concentration C'A ; pKa ( NH4+ / NH3) = 9,2). On titre un volume VA= 10,0 mL de solution S par une solution d’hydroxyde de sodium (Na+ +HO-) de concentration CB = 1,00.10-1 mol.L-1 ; pKa ( H2O / HO-) = 14). On note VB le volume de solution titrante ajoutée à la burette. On propose de comparer les résultats de trois techniques de dosage : • Dosage pH-métrique (courbe 1 : pH = f(VB)) ; • Dosage conductimétrique (courbe 2 : ) s* = s (VA+VB) / VA = f(VB), où σ est la conductivité de la solution et *σ la conductivité corrigée ; σ et *σ sont exprimés en mS.m-1). 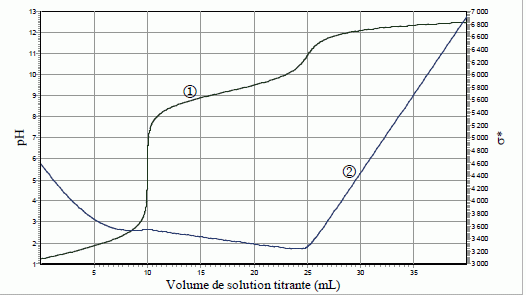 Proposer un schéma détaillé et légendé (nature de la verrerie, des électrodes, …) permettant d’effectuer simultanément les titrages pH-métrique et conductimétrique. 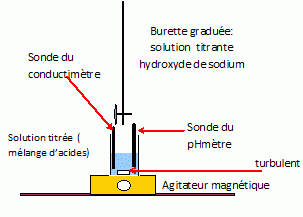 Sonde du pHmètre : électrode combinée ( électrode de verre + électrode de référence) L'extrémité de la sonde du conductimètre doit être suffisamment immergée : il faut ajouter 200 mL d'eau distillée dans le becher. Indiquer quelles sont les trois réactions qui ont lieu au cours du dosage, en précisant les valeurs de leurs constantes d’équilibre. Préciser celle(s) qui se déroule(nt) avant la première équivalence, puis ce qui se passe entre les deux équivalences. La première acidité de l'acide sulfurique est forte : H3O+aq + HO-aq = 2H2O ; K1 = 1014. Couples acide / base : HSO4- / SO42- et H2O / HO-aq HSO4- aq + HO-aq = SO42- aq + H2O ; K2 = 1014-2= 1012. Ces réactions se déroulent avant la première équivalence. Entre les deux équivalences : Couples acide / base : NH4+ / NH3 et H2O / HO-aq NH4+ aq + HO-aq =NH3 aq +H2O ; K3 = 1014-9,2= 104,8. Déterminer graphiquement les volumes des points d’équivalence. Indiquer à chaque fois la courbe exploitée. 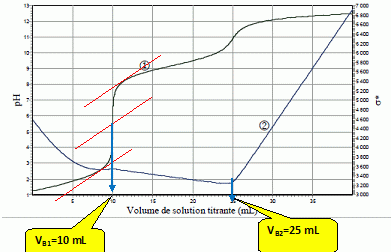 1ère équivalence : on exploite la courbe 1, sut de pH important. Seconde équivalence : on exploite la courbe 2 ( conductimétrie) ; le saut de pH est trop faible pour être exploitable. En déduire les valeurs des concentrations CA et C'A. 2CAVA =CB VB1 ; CA =CB VB1 / (2VA ) = 1,00.10-1 *10 / 20 = 5,00.10-2 mol/L. VB2 -VB1 = 15 mL de soude nécessaire pour doser NH4+ : C'A =CB VB3 / VA = 1,00.10-1 *15 / 10 = 1,50 10-1 mol/L. Justifier qualitativement l’augmentation de la conductivité après la deuxième équivalence. Dans le becher, après la seconde équivalence, on ajoute des ions hydroxyde ( cesux-ci sont en escès ) et des ions sodium ; la conductivité molaire ionique des ions hydroxyde est importante, la conductivité de la solution va croître. Aurait-il été possible d’utiliser un indicateur coloré pour repérer le 1er point d’équivalence ? le 2ème point d’équivalence ? Si oui le(s)quel(s) ? La zone de virage de l'indicateur coloré doit contenir le pH du point équivalent : 1ère équivalence : pHE ~5,5 : le rouge de méthyle convient. Seconde équivalence : pHE ~11,5 : le jaune d'alizarine convient.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|