Etude de l'accéléromètre d'un stabilisateur d'images concours Mines 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Les appareils photo reflex numériques, même ceux d’entrée de gamme, sont aujourd’hui équipés d’accéléromètres pour la stabilisation d’image. Cela permet, en particulier sur les longues focales, de stabiliser la visée. Il est alors plus facile de faire le point sur un sujet très lointain et il est plus aisé de soigner son cadrage, les tremblements du photographe étant amortis. On se propose, dans cette partie, d’étudier le fonctionnement d’un accéléromètre à détection capacitive, ce système étant le plus répandu actuellement. 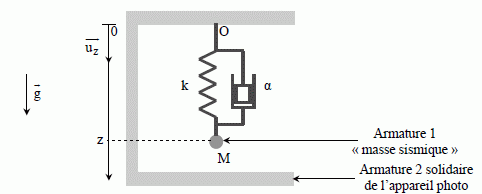Son principe est décrit ci-après : Une poutre suspendue appelée « masse sismique » constitue l’une des armatures d’un condensateur plan. L’autre armature est solidaire de l’appareil photo dont on veut mesurer l’accélération (voir figure ). Les variations de capacité liées au déplacement de la masse sismique permettent de suivre son mouvement. 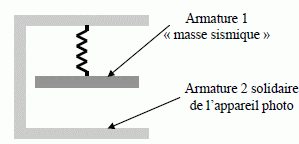Les vecteurs sont écrits en gras et en bleu. On modélise la structure mécanique étudiée par une masse ponctuelle M de masse m, suspendue à l’extrémité d’un ressort de constante de raideur k et de longueur à vide l0, dont l’autre extrémité est fixée en O au bâti solidaire de l’appareil photo (voir figure ). Les amortissements sont modélisés par une force de frottement de la forme : f = -avM où vM représente la vitesse du point M dans le référentiel de l’appareil photo. On s’intéresse à la détermination de l’amplitude Z0 de la vibration engendrée par le tremblement du photographe. On considère pour cela que le point O oscille verticalement à la pulsation ω avec une amplitude Z0 dans le référentiel terrestre considéré comme galiléen. Sa position y est repérée par sa cote zO(t)=Z0cos(ωt). La position de la masse M est repérée dans le référentiel de l’appareil photo par sa cote z. On note zeq la position d’équilibre de la masse M par rapport à l’appareil en l’absence de vibration. Déterminer son expression en fonction de l0, m, g et k. La masse M est en équilibre sous l'action de son poids et de la tension du ressort. Poids : mg ; tension  : T = k(zeq -l0 ) ; mg = k(zeq -l0 ) zeq =mg/k +l0. Etablir l’équation différentielle du mouvement de la masse M dans le référentiel de l’appareil photo en faisant apparaître les paramètres α, k, m, zeq, ω et Z0. La masse M est soumise  à  : - son poids, verticale vers le bas, valeur mg : P = mg uz. - la force de rappel exercée par le ressort F = -k(z-zO-l0) uz. - la force de frottement de la forme : f = -avM oscillations forcées : le support et la masse m sont en mouvement. 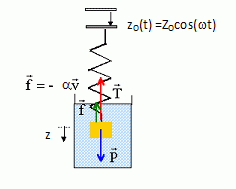Ecrire la seconde loi de Newton : P +F +f = m a. Soit suivant l'axe Oz : mg-k(z-zO-l0)-avM = m a ; vM =dz/dt = z' ; a = d2z/dt2 = z" m z" + a z' +k(z-l0) =mg+kzO z" +a /m z' +k(z-l0)/m = g+k/mzO. On note Z = z – zeq la position de la masse M par rapport à sa position d’équilibre dans l’accéléromètre. z-l0= z-zeq+zeq-l0 = Z +zeq-l0 =Z+mg/k k(z-l0) = kZ +mg ; k(z-l0)/m =kZ/m+g ; de plus Z' = z' et Z" = z" L'équation différentielle s'écrit : Z" +a /m Z' +kZ/m = k/mzO. Z" +a /m Z' +kZ/m = k/mZ0cos(ωt).   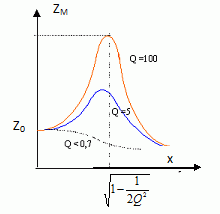Web www.chimix.com Montrer que l’équation du mouvement de M peut se mettre sous la forme : Z" +w0/Q Z' +w02Z =Z0w02 cos(wt). Nommer w0 et Q. Préciser leurs dimensions et leurs expressions en fonction de m, α et k. Z" +a /m Z' +kZ/m = k/mZ0cos(ωt). (1) On pose w02 = k/m. w0  = pulsation propre  exprimée en rad s-1. Par suite : Z" +a w02 / k Z' +w02 Z = w02Z0cos(ωt). On identifie : 1/Q = a w0 / k ; Q = k/( a w0 ). Q facteur de qualité exprimé en : w0/Q Z' a la dimension d'une accélération : longueur  divisée par le carré d'un temps. Z' a la dimension  d'une longueur divisée par un temps : [w0/Q] = T-1 ; [w0] = T-1 ; Q est sans dimension. On s’intéresse maintenant au mouvement de la masse en régime établi. Expliquer pourquoi Z(t) peut se mettre sous la forme Z(t)=ZMcos(ωt +j). Préciser la signification des différents termes apparaissant dans cette expression. La solution de l'équation différentielle sans second membre est amortie exponentiellement : elle correspond à un régime transitoire. La solution particulière  de cette équation différentielle correspond au régime permanent. On se place au bout d'un temps suffisamment long pour que le régime permanent soit atteint : la solution de l'équation sans second membre est alors négligeable devant la solution particulière. L'excitateur force l'oscillateur à osciller à la fréquence de l'excitateur. ZM : amplitude de la masse M ; ω : pulsation de l'excitateur ;  j : déphasage. Etablir l’expression de ZM en fonction de ZO, Q et de la pulsation réduite x=ω / w0. Il est conseillé d’utiliser les notations complexes. Z(t)=ZMcos(ωt +j) s'écrit en notation complexe : Z =ZM exp(jj) exp (jw t). dérivées : Z' = ZM exp(jj) jw exp(jw t) ; Z" = ZM exp(jj) (-w²) exp(jw t) ; repport dans Z" +w0/Q Z' +w02Z =Z0w02 cos(wt) : -ZM exp(jj) w² exp(jw t) +w0/Q ZM exp(jj) jw exp(jwt) + w0² ZM exp(jj) exp(jw t)= Z0w02 exp(jw t) simplifcation par exp(jw t) : ZM exp(jj) (w0² -w² )+w0/Q jwZM exp(jj) = Z0w02 ZM [ (w0² -w² )+w0/Q jw ]=Z0w02exp(-jj) Diviser tous les termes par w02 et remplacer ω / w0 par x. ZM [(1-x² )+jx/Q] =Z0exp(-jj) Module du nombre complexe du membre de gauche  = module du nombre complexe  du membre de droite ZM  [(1-x² )2 +(x/Q)2 ]½ =Z0   ZM =Z0 /[(1-x² )2 +(x/Q)2 ]½.  Quelle est la nature du filtre associé à ZM(x) ? Filtre passe bande. Montrer que la courbe ZM(x) passe par un maximum pour Q > 2-½ et préciser l’expression xr de x lorsque ZM passe par ce maximum. Comparer xr et 1. Dériver ZM par rappot à x en posant u = (1-x² )2 +(x/Q)2  soit dZM / dx = Z0 (-0,5 u' u -1,5). u' = (1-x² )(-4x) +2x/Q2 = 2x [(1/Q2 -2(1-x² )] s'annule pour x=0  ; de plus : x2= 1-1/(2Q2) ;  ( 1-1/(2Q2) doit être positif soit Q supérieur  à 2-½ ) de plus ZM tend vers Z0 quand x tend vers zéro et ZM tend vers 0 quand x tend vers l'infini donc l'amplitude ZM passe par une valeur maximale quand x2= 1-1/(2Q2) ; xr = [1-1/(2Q2) ]½. xr est d'autant plus proche de 1 que Q est grand ( résonance aigüe) Etudier les asymptotes basse et haute fréquences de ZM(x) puis tracer sur un même graphique l’allure de la courbe ZM(x) pour Q1 <2-½, Q2 >2-½ et Q3 > Q2 en portant une attention particulière au positionnement des maxima.  ZM tend vers Z0 quand x tend vers zéro et ZM tend vers 0  quand x tend vers l'infini. Comment faut-il choisir le facteur de qualité du système et sa pulsation propre pour qu’il fonctionne sur une plage de fréquences de tremblements la plus large possible ? La bande passante w0/Q doit être assez grande. Le facteur de qualité doit donc être faible. La pulsation propre doit  correspondre  à  la pulsation moyenne des tremblements.

retour -menu