Etude d'un appareil photographique concours Mines 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Ce problème aborde le fonctionnement de quelques éléments d’un appareil photographique dans trois parties indépendantes. La première traite de la constitution optique d’un téléobjectif, la seconde détaille le fonctionnement d’un flash électronique et la dernière propose une modélisation mécanique d’un accéléromètre intervenant dans le dispositif de stabilisation de l’image.  Les résultats des applications numériques seront présentés avec deux chiffres significatifs.  Partie A : Etude d’un téléobjectif. Un téléobjectif est un objectif de longue focale, c’est-à-dire un objectif dont la focale est supérieure à la diagonale de la pellicule pour un appareil photographique argentique ou de la matrice de cellules photosensibles dans le cas d’un appareil photographique numérique. Ces objectifs permettent un cadrage serré des sujets photographiés grâce à un angle de champ étroit. Dans les trois parties suivantes, largement indépendantes, le sujet photographié est constitué par la tour Eiffel culminant à une hauteur h = 324 m du sol et située à une distance d = 2,0 km du photographe. Partie A1 : Objectif standard On s’intéresse dans un premier temps à un objectif standard d’appareil photographique argentique constitué d’une lentille convergente unique de centre O et de focale f’ = 50 mm. Quelle doit être la distance D entre la lentille et la pellicule pour que la photographie soit nette ? Justifier votre réponse. L'objet est  à l'infini ( d = 2,0 km est très supérieure à f' = 50 mm ). L'image nette se forme dans le plan focale image de la lentille : D = 50 mm. Construire sur un schéma l’image de l’objet sur la pellicule (sans respecter l’échelle). On appelle h1 la hauteur de l’image de la tour Eiffel sur la pellicule. Déterminer son expression en fonction de f’, d et h puis calculer sa valeur numérique. 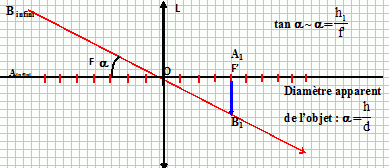h1 = h f'  /d =324*0,050 / 2,0 103 =8,1 10-3 m = 8,1 mm. Partie A2 : Réalisation d’un téléobjectif avec une lentille unique. Expliquer pourquoi, si l’on souhaite photographier les détails d’un sujet lointain, il faut choisir un objectif de focale plus élevée que celle d’un objectif standard. L'objectif standard donne d'un objet lointain de grande dimension, une image de 8 mm de haut. Cette lentille donnerait d'un détail de 1 m de dimension  une image de hauteur 2,5 10-2 mm : ce détail serait invisible. Dans le cas d’un téléobjectif de focale f’0 = 200 mm, calculer la hauteur h2 de l’image de la tour Eiffel sur la pellicule ainsi que l’encombrement de l’appareil (distance entre la lentille et la pellicule) La distance entre la lentille et la pellicule  est  : 200 mm = 20 cm. h2 = h f'0  /d =324*0,200 / 2,0 103 =3,24 10-2 m = 32 mm. La matrice de cellules photosensibles de la plupart des reflex numériques est plus petite que la surface impressionnable de la pellicule d'un reflex 24x36. Justifier alors pourquoi un téléobjectif de focale donnée permet un cadrage plus serré du sujet avec un appareil numérique qu’avec un appareil argentique. L'angle de champ "A" est donné par la relation : tan ( ½A) = L/(2f') avec f' : distance focale et L : dimension de la matrice  de cellules photosensibles ou de la pellicule . A focale donnée, l'angle de champ est plus faible si les dimensions de la matrice de cellules photosensibles  sont  inférieures à celles de la pellicule A un angle de champ plus petit correspond un cadrage plus serré. On considère dans un premier temps une lentille de verre d’indice n placée dans l’air. On se place dans l’approximation d’un indice n ne dépendant pas de la longueur d’onde. Reproduire la figure  et tracer la marche du rayon incident représenté dans et après la lentille. Justifier sommairement le tracé. Loi de Descartes pour la réfraction sur la face d'entrée : nair sin i1 = n sin i2. l'angle d'incidence i1 étant nul, l'angle de réfraction i2 est nul. Loi de Descartes pour la réfraction sur la face de sortie : n sin i'1 =nair sin i'2. n >nair conduit  à i'1 < i'2. Quelle est la nature de cette lentille ? Justifier. La lentille est plus épaisse au centre que sur les bords : il s'agit d'une lentille convergente. Définir le foyer image d’un système optique. Indiquer sur la figure le foyer image F’de la lentille. Le foyer image est l'image d'un objet  situé  à l'infini. C'est le point de convergence d'un faisceau incident parallèle à l'axe optique, après traversée de la lentille. L’indice de réfraction n du verre constituant la lentille dépend en réalité de la longueur d’onde λ de la radiation lumineuse qui la traverse. 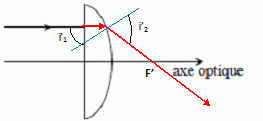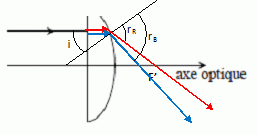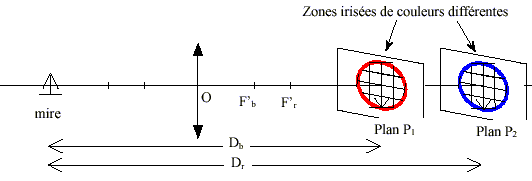Ils sont reliés par la loi de Cauchy : n(l)=a + b / l2 où a et b sont des constantes positives qui ne dépendent que du milieu traversé. Comparer rR et rB, angles réfractés en sortie de lentille pour une radiation rouge et pour une radiation bleue en considérant des rayons incidents parallèles à l’axe optique. Tracer alors les chemins suivis par ces deux radiations dans et après la lentille. La longueur d'onde d'une radiation bleue est inférieure  à celle d'une radiation rouge. L'indice de réfraction du bleu nB est donc supérieur à l'indice nB d'une radiation rouge. Il n'y a pas de déviation sur la face d'entrée ( faisceau incident perpendiculaire  à la face ). Loi de Descartes pour la réfraction sur la face de sortie s'écrit :  nB sin i =nair sin rB   : sin rB  = nB sin i et  nR sin i =nair sin rR :  sin rR = nR sin i Or nB > nR donc rB  > rR. Expliquer le problème qui pourrait se poser si l’on réalisait un téléobjectif avec une lentille unique. Aberration chromatique : dispersion subie par la lumière polychromatique réfractée par le verre. En déplaçant l’écran, on a obtenu une image tantôt irisée en rouge, tantôt irisée en bleu comme montré sur le schéma ci-dessous. On peut s’affranchir de ce problème en réalisant un doublet, équivalent à une lentille convergente unique, constitué d'une lentille convergente accolée à une lentille divergente, les deux lentilles étant taillées dans des verres d’indices de réfraction différents. Le téléobjectif ainsi constitué présente toutefois l’inconvénient d’un encombrement important.   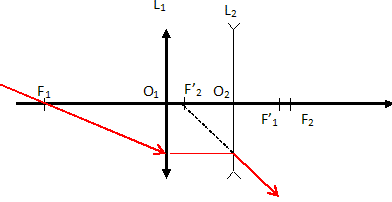Web www.chimix.com Réalisation d’un téléobjectif par association de deux lentilles distantes de e. Afin de raccourcir les téléobjectifs, en particulier les plus puissants, on peut réaliser un autre montage en associant deux lentilles distantes d’une distance e : une lentille convergente L1 de centre O1 et de focale f’1 et une lentille divergente L2 de centre O2 et de focale f’2. On prendra pour les applications numériques : f’1 = 50 mm, f’2 = -25 mm et e = O1O2 = 31 mm. On note P l’intersection du plan de la pellicule avec l’axe optique et F’ l’image par le téléobjectif d’un point à l’infini sur l’axe optique. Déterminer littéralement la position de F’en fonction de f’1, f’2 et e. expression de la matrice de transfert : matrice de réfraction sur le dioptre L2 V2 : vergence matrice de translation O1O2 = e milieu d'indice n =1 matrice de réfraction sur le dioptre L1 V1 : vergence 1 ; 0 -V2 1 1 ; e /n 0 1 1 ; 0 -V1 1 matrice de transfert du doublet : 1 -eV1 ;............ e -(V1+V2-eV1V2) ; 1-eV2. vergence du doublet : V = V1+V2-eV1V2. 1/F' = 1/f'1 + 1/f'2 - e /(f'1f'2). En déduire l’expression de l’encombrement O1P de l’appareil en fonction de ces mêmes grandeurs. Après l’avoir calculé approximativement, déterminer laquelle de ces trois valeurs : O1P = 14 cm, O1P = 11 cm et O1P = 8,0 cm correspond à l’encombrement du téléobjectif. L'image d'un objet  à l'infini se trouve dans le plan focal image du doublet : O2F' =F'( 1-eV1) O1P = O1O2+O2F' = e + O2F' 1/F' = 1/0,050 + 1/ (-0,025) - 0,031/(0,050*(-0,025)) =20-40+24,8 = 4,8  ; F' = 0,208 m. O2F' =F'( 1-eV1)  = 0,208(1-0,031*20)=0,079 m O1P =e + O2F' =0,031+0,079 =0,11 m = 11 cm. Déterminer l’expression de h3, hauteur de l’image de la tour Eiffel sur la pellicule en fonction de f’1, f’2, e, d et h.  Après l’avoir calculée approximativement, déterminer laquelle de ces trois valeurs : h3 = 14 mm, h3 = 34 mm et h3 = 54 mm correspond à la hauteur de l’image sur la pellicule. Dans l'expression ci-dessus h1 = h f'  /d  remplacer f' par F' telle que : 1/F' = 1/f'1 + 1/f'2 - e /(f'1f'2). h3 = h F'  /d=324*0,208 / 2,0 103 =3,37 10-2 m = 34 mm. Commenter les résultats précédents. L'association de deux lentilles distante de e : - réduit l'encombrement - tout en donnant une image la plus grande possible.

retour -menu