Mécanique : oscillateur élastique, frottement solide concours Mines 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

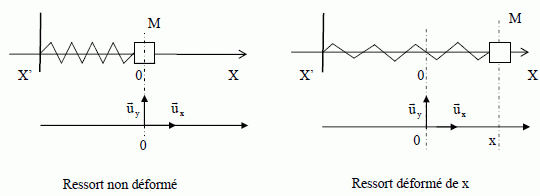
Une particule M de masse m peut glisser sur un rail horizontal X'X dans le référentiel terrestre supposé galiléen.. M est fixée  à l'extrémité d'un ressort de raideur k dont l'autre extrémité est fixe. La position de M est repérée par son abscisse x. x=0 correspond au ressort détendu. Le glissement s'effectue, dans un premier temps sans frottement. Représenter sur un dessin, les forces exercées sur M dans le cas où x >0, faire le bilan de ces forces, puis par application de la relation fondamentale de la dynamique, déterminer l'équation différentielle vérifiée par x(t). 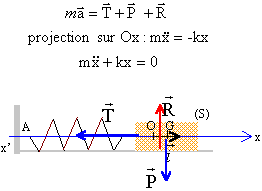Le solide est soumis à 3 forces : P :action gravitationnelle de la Terre sur le solide (poids du solide). R action normale de la piste sur le solide.on néglige les frottements. T: tension, action du ressort sur le solide. Donner l'expression de l'énergie potentielle élastique emmagasinnée dans le ressort en fonction de k et x. Ep = ½k x2. Exprimer l'énergie mécanique du système { masse + ressort } en fonction de m, k, x et de sa dérivée x'. Est-elle conservée au cours du mouvement ? Justifier. L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. Le système est soumis  uniquement  à des forces conservatives ( pas de frotements) : l'énergie mécanique se conserve. EM = ½mx'2 + ½kx2. De ce qui précède, déduire  à nouveau l'équation différentielle du mouvement de M. Dériver EM par rapport au temps : 0 = mx' x'' + k x x' simplifier par x' : 0 = mx"+kx. Résoudre l'équation différentielle et obtenir l'équation horaire x(t) du mouvement de M dans le cas où M est lancé  à t=0 de l'abscisse x0 avec la vitesse  v0 = x'0 ux ( les grandeurs en bleu et gras sont des vecteurs). x(t) est de la forme x(t) = A sin ( w0t+j) avec w0 = (k/m)½. x'(t) = A w0 cos ( w0t+j) x'(0) = A w0 cos ( j) = x'0 d'où cos ( j) = x'0 / (A w0). x(0) = A sin (j) = x0 d'où : sin (j) = x0 / A. par suite tan (j) =x0w0 /x'0. cos2 ( j) +sin2 ( j) = 1 ; [x'0 / (A w0)]2 +[x0 / A]2 =1 ; A2 =(x'0 / w0)2 +x02  ; A = [(x'0 / w0)2 +x02 ]½.   Web www.chimix.com Maintenant M est soumise de la part du rail à une force de frottement  solide f de norme constante f quand  M est en mouvement et comprise entre 0 et f quand M est immobile. Grâce  à un schéma des forces quand M est en mouvement, et en précisant le sens du mouvement, déterminer l'angle j entre la réaction du support et la verticale en fonction de m, g et f.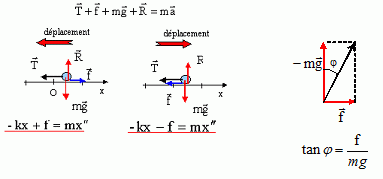 On donne  à M l'élongation ( l'abscisse ) x0 positive ou négative et on l'abandonne sans vitesse. A quelles conditions sur x0, M démarrera t-elle ? M démarre si la valeur de la force de rappel exercée par le ressort est supérieure à la valeur de la force de frottement. kx0 > f. Entre quelle limites de x se  situera donc la  position d'équilibre finale de M ? M s'arrête si la valeur de la force de rappel exercée par le ressort est inférieure à la valeur de la force de frottement. kx0 < f ; x1 = f/k ; x2 = -f/k. Du fait que les frottements n'ont pas toujours le même sens, montrer que la force de frootement f peut s'écrire  f = -e f ux, où  le coefficient e vaut +1 si dx/dt >0 et -1 si dx/dt<0. Ecrire  alors l'équation différentielle du mouvement de M sans la résoudre. Si dx/dt est positif, le solide  se déplace dans le sens de l'axe ; la force de frottement est dans le sens contraire de l'axe. L'équation différentielle s'écrit : mx" = -kx -f ; mx" + kx = -f. Si dx/dt est négatif, le solide  se déplace dans le sens contraire de l'axe ; la force de frottement est dans le sens  de l'axe. L'équation différentielle s'écrit : mx" = -kx +f ; mx" + kx = +f. Pour toute la suite du problème on prendra x0 positif est très supérieur  à la limite de démarrage de M, de telle façon que M effectue plusieurs oscillations. Ecrire puis résoudre l'équation différentielle sur l'intervalle [x0 ; x1] où x1 est l'abscisse de M lorsqu'il s'arrête pour la première fois. mx"+kx =+f ; x"+k/m x = + f/m (1) ;  on pose w02 = k/m. Solution générale de l'équation sans second membre : x(t) = A cos (w0t +j) Solution particulière de (1) : x = +f/k Solution générale de (1) : x(t) = A cos (w0t +j)+f/k A t = 0, x(0) = x0=   A  cos j +f/k. vitesse  dx/dt = -Aw0 sin (w0t +j) La vitesse initiale est nulle : [dx/dt ]0= 0 = -Aw0 sin j ; Aw0  n'est pas nul  donc sin j  soit j =0. par suite A = x0-f/k. x(t) = (x0-f/k) cos (w0t)+f/k. Quelle est la durée de cette première étape ? Trouver la valeur de x1. La vitesse s'annule pour la première fois  à la date t1 : [dx/dt ]t1= 0 =-(x0-f/k)w0 sin (w0t1) ; sin (w0t1) = 0 ; w0t1 =  p ; t1 =  p /w0 = ½T0. x1 = (x0-f/k) cos (w0t1)+f/k ;  x1 = (x0-f/k) cos (p)+f/k ; x1 = - (x0-f/k)+f/k ; x1 = - x0+2f/k. Le phénomène se produisant de x1 à x2 où M s'arrête à nouveau, etc..., le mouvement de M est pseudopériodique. Déterminer la pseudo-période des oscillations. mx"+kx =-f ; x"+k/m x = - f/m (2) ;  on pose w02 = k/m. Solution générale de l'équation sans second membre : x(t) = A cos (w0t +j) Solution particulière de (2) : x = -f/k Solution générale de (2) : x(t) = A cos (w0t +j)-f/k A t = t1 , x(t1 ) = x1=   A  cos(p+ j )-f/k. vitesse  dx/dt = -Aw0 sin (w0t +j) La vitesse  à la date t1 est nulle : [dx/dt ]t1= 0 = -Aw0 sin (p+ j ) ; Aw0  n'est pas nul  donc sin  (p+ j )   soit j =0. par suite A = -x1-f/k =x0-3f/k. x(t) = (x0-3f/k) cos (w0t)-f/k. La vitesse s'annule pour la seconde fois  à la date t2 : [dx/dt ]t2= 0 =-(x0-3f/k)w0 sin (w0t2) ; sin (w0t2) = 0 ; w0t2 =  2p ; t2 =  2p /w0 = T0. La pseudo-période des oscillations est égale  à  la période propre T0. x2 = (x0-3f/k) cos (w0t2)-f/k ;  x2 = (x0-3f/k) cos (2p)-f/k ; x2 = (x0-3f/k)-f/k ; x2 = x0-4f/k. Exprimer le travail de f sur le parcours [x1, x2] en fonction de f, x1 et x2. Sans rechercher  à nouveau l'équation horaire du mouvement de M, déterminer grâce au théorème de l'énergie cinétique, l'élongation x2 quand M s'arrête pour la deuxième fois. ( en fonction de x0, f et k). La vitesse initiale en x2  et la vitesse finale en x1 sont nulles ( arrêt) : la variation d'énergie cinétique est nulle. Seules la force exercée par  le ressort et les frottement travaillent : Travail de la force exercée par le ressort : ½kx12-½kx22 ; travail des frottements : -f(x2-x1) ½kx12-½kx22 -f(x2-x1) =0 avec x1 négatif. ½k(x1-x2)(x2+x1)-f(x2-x1) =0 ½k(x2+x1) +f=0 ; x2 = -x1 -2f/k. Or x1 = -x0+2f/k d'où : x2 = x0 -4f/k. De l'étude qui précède, déduire la nature de la décroissance de l'amplitude du mouvement au cours du temps. Déterminer l'équation xmax(t) de la courbe reliant les maxima de x. Les valeurs extrêmes atteintes sont sur une courbe linéaire, appelée l'enveloppe du graphe de x(t). xmax(t) = x0 -4f/k t ou xmax(t) = -x0 +4f/k t.

retour -menu