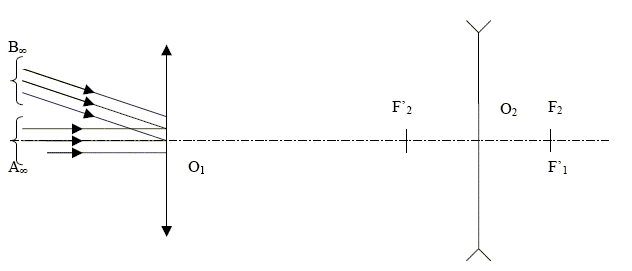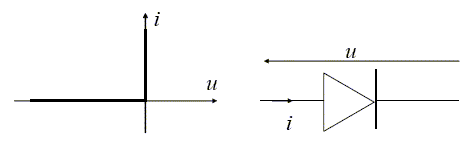Observation des anneaux de Saturne : lunette afocale, prise de vue numérique physique concours Mines 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Un astronome pointe sa lunette vers Saturne dans le ciel nocturne dégagé : on assimile cette planète à une source de lumière très éloignée, notée Aoo, et une portion de l’anneau le plus brillant à une autre source notée Boo. Ces deux sources sont séparées par une zone sombre. La lunette reçoit de chacune de ces deux sources des faisceaux de rayons parallèles, l’axe de la lunette étant parallèle à ceux venant de Aoo. Le rayon de l'anneau est de l'ordre de RA = 108 m, la distance entre la Terre et Saturne est de l'ordre de D = 1,5 1012 m. On note a l’angle entre les deux direc-tions. La lunette forme un système afocal, c’est-à-dire qu’il ne possède pas de foyer : deux rayons incidents parallèles émergent parallèlement du système optique. Elle est constituée de deux lentilles minces : la première, l’objectif, a pour centre O1 et pour vergence V1 = 1/f'1 = +1,0 d ; la seconde, l’oculaire, a pour centre O2 et pour vergence V2 = 1/f'2 = -5,0 d ; elles sont écartées de O1O2 = 80 cm. La figure 1, complétée, sera rendue avec la copie : l’échelle sur l’axe est 1/10 et l’angle a est volontairement exagéré. Les conditions de Gauss sont supposées vérifiées. 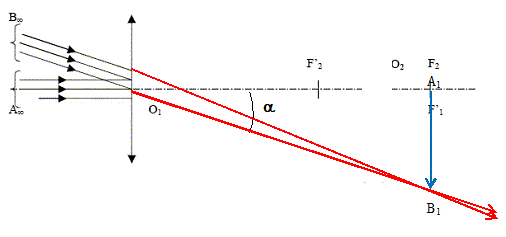Calculer numériquement l’angle a.  tan a = RA / D = 108 / 1,5 1012 = 6,7 10-5 rad ; a étant petit, tan a ~ a =6,7 10-5 rad. Construire l’image A1B1 de AooBoo par l’objectif. Est-ce une image réelle ou virtuelle ? Sera-t-elle considérée comme un objet réel ou virtuel pour l’oculaire ? L'image d'un objet à l'infini se trouve dans le plan focal image de l'objectif : O1A1 = f'1 = 1,0 m. Etant située à droite de l'objectif, c'est une image réelle. O1O2 = 0,8 m, A1B1 est à droite de l'oculaire : A1B1 jour le rôle d'un objet virtuel pour la seconde lentille. Tracer des rayons émergents issus de et A1B1 après traversée de l’oculaire. Expliquer pourquoi cette lunette est bien afocale. A1B1 joue le rôle d'objet pour l'oculaire. A1B1 étant au foyer objet de la seconde lentille, l'image définitive est à l'infini. Le faisceau émergent de la lunette est parallèle ; le faisceau incident est parallèle : la lunette est donc afocale. 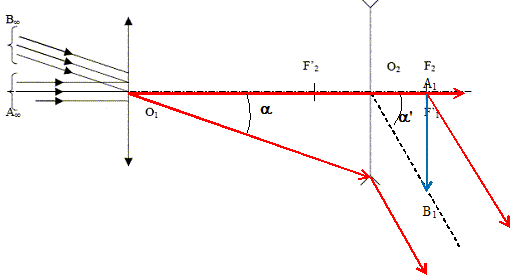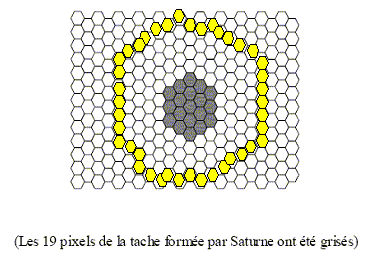On note a' l’angle entre la direction des faisceaux de rayons émergents issus de Aoo et celle des rayons émergents issus de Boo. On appelle grossissement le rapport G =a/a'. Exprimer la valeur absolue de G en fonction de f'1 et f'2 et la calculer numeriquement. tan a ~a = A1B1 /f'1 ; tan a' ~a' = A1B1 /|f'2| ; G = f'1 /|f'2| =1/0,2 =5. L’oeil, sans instrument d’optique, ne peut distinguer deux rayons que si l’angle qui les sépare est supérieur ou égal à a0= 1,0 10-4 rad. (c’est le pouvoir séparateur de l’oeil). Vérifier que l’utilisation de la lunette est indispensable pour distinguer les anneaux de Saturne. a =6,7 10-5 rad ; a0= 1,0 10-4 rad ; a <a0 : les anneaux ne peuvent pas être distingués à l'oeil nu. avec la lunette a' = 5 a = 5*6,7 10-4 =3,3 10-4 rad ; a' >a0 : les anneaux peuvent être distingués. Une caméra numérique remplace l’oeil derrière l’oculaire : elle est constituée par une lentille convergente de vergence V3 = +50 dioptries (remplaçant le cristallin) et une plaque tapissée de cellules photosensibles en nid d’abeille distantes de 1µm (remplaçant les cellules de la rétine) placée dans le plan focal de la lentille. Sur la figure 2, on a noirci les cellules recevant de la lumière venant de la planète Saturne elle-même (où il apparaît qu’elle n’est pas réellement ponctuelle car son image occupe plusieurs pixels) ; noircir les cellules qui recevront de la lumière venant de l’anneau (on suppose qu’il est vu de face et de faible largeur). En déduire pourquoi on peut effectivement reconnaître la forme d’un anneau. A'B' =a' f'3 =3,3 10-4 /50 =6,6 10-6 m = 6,6 µm, soit environ six cellules, et cela dans toutes les directions. 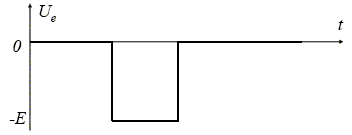Etude des cellules de l’appareil de prises de vue numérique. 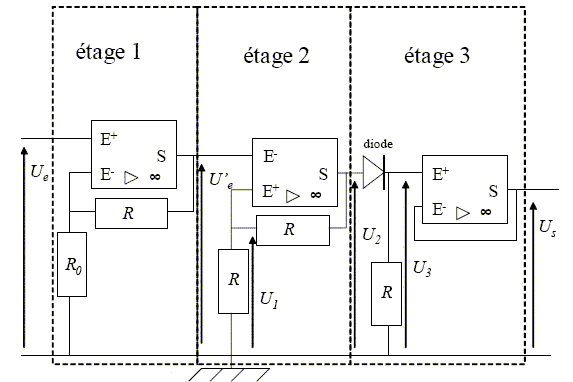Les cellules de l’appareil de prises de vue numérique convertissent une impulsion lumineuse reçue au moment de la prise de vue en une impulsion électrique : • si la cellule reçoit de la lumière au-dessus d’un certain seuil, la tension de sortie, notée Ue ci-dessous, décrit un créneau, formé d’un échelon descendant de tension suivi d’un échelon remontant de tension : 0 --> -E -->0 ; si la lumière reçue par la cellule reste en-dessous du seuil (ce qui correspond à l’obscurité), la tension de sortie reste à la valeur 0. L’électronique de traitement de l’information, intégrée dans l’appareil, a alors plusieurs rôles, dont nous tirons deux étapes essentielles : • l’amplification du signal électrique lorsque la cellule a reçu de la lumière au-dessus du seuil ; • la mise en mémoire de l’information : on souhaite conserver durablement, après la prise de vue, une tension dont la valeur soit représentative de l’état de la cellule lors de la prise de vue : 0 V correspond à une cellule ayant reçu moins de lumière que le seuil « obscurité », +15 V correspond à une cellule ayant reçu une impulsion lumineuse au-dessus du seuil « lumière ». Ces deux fonctions sont réalisées par le montage suivant qui comprend trois étages.   Tous les amplificateurs opérationnels sont idéaux, de gain infini, de tension de saturation Vsat = +15 V. Les résistors notés R ont une résistance R= 50 kW. La diode est idéale : la tension à ses bornes est nulle lorsqu’elle est passante, le courant qui la traverse est nul lorsqu’elle est bloquée, lorsque le potentiel à son entrée est strictement inférieur à celui à sa sortie ; sa caractéristique est rappelée ci-après. 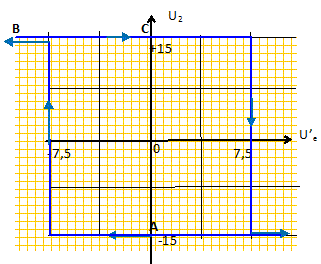Les étages 1 et 2 diffèrent par l’entrée sur laquelle est branchée la boucle de contre-réaction : sur l’entrée inverseuse dans le 1 et sur l’entrée non inverseuse dans le 2 ; quelle est la conséquence fondamentale de cette différence dans le régime de fonctionnement des deux amplificateurs opérationnels ? Etage 1 : fonctionnement en régime linaire, la contre réaction est branchée sur E-. Etage 2 : fonctionnement en régime saturé, la contre réaction est branchée sur E+. Si V+ >V- alors VS = + 15 V ; si V- >V+ alors VS = - 15 V. Étude de l’étage 1. Expression de la tension U'e en fonction de la tension Ue et des résistances R et R0. Ecrire le théorème de Millmann en E- : VS/R = VE-(1/R0+1/R) =(R+R0)VE- / (R0R) ; VS= (R+R0)VE- /R0 = (R/R0+1)VE- ; or VS= U'e et VE- =VE+ =Ue soit : U'e =(R/R0+1)Ue. En déduire le nom de la fonction réalisée par cet étage. amplificateur non inverseur. La tension d’entrée Ue ne peut prendre que les valeurs 0 V et -50 mV. On veut que la tension U'e puisse prendre les valeurs 0 V et -10 V. En déduire la valeur de R0. 10 = (50 /R0 +1)*0,05 ; 200 = 50 /R0 -1 ; R0 =50 / 201 ~0,25 kW. Étude de l’étage 2. Exprimer la tension U1 en fonction de la tension U2. L'intensité dans l'entrée E+ est nulle ; les deux résistances R sont en série et traversées par le courant d'intensité i, d'où Ri + Ri = U2. De plus Ri = U1 : U1 = œU2. U2 ne peut prendre que deux valeurs : -15V et +15 V, donc U1 prendra les deux valeurs -7,5 V et + 7,5 V. On isole cet étage du reste du circuit et on suppose que l’on fait varier continûment U'e de la valeur -10 V à la valeur +10 V puis de la valeur +10 V à la valeur -10 V. Déterminer, en justifiant brièvement, les variations de U2 lors de ce cycle. si U1 -U'e>0, U2 = + 15 V ; si U1 -U'e<0, U2 = - 15 V ; U'e=-10V ; U1 -U'e>0 : U2 = + 15 V ; U1 = 7,5 V. U'ecroît et atteint, dépasse 7,5 V, U1 -U'e<0 : U2 = - 15 V ; U1 = -7,5 V. U'e décroît de +10 V et atteint, dépasse -7,5 V, U1 -U'e>0 : U2 = + 15 V ; U1 = +7,5 V. Tracer l’allure de la courbe dans un diagramme où U'e figure en abscisse et U2 en ordonnée. En déduire le nom de la fonction réalisée par cet étage. comparateur à hystérésis. Avant la prise de vue, Ue= 0 V et on impose U2 = -15 V grâce à un dispositif non représenté sur le schéma (la fonction RESET). Montrer que • si la cellule reçoit moins de lumière que le seuil, U2 restera bloquée à -15 V après la prise de vue, On part du point A, U'e=Ue = 0 V, U1 = -7,5 V et en conséquence U1 -U'e<0 : U2 = - 15 V. • si la cellule reçoit une impulsion lumineuse au-dessus du seuil, U2 restera bloquée à +15 V après la prise de vue. U'e= -10 V, U1 = -7,5 V : U1 -U'e>0 : U2 = + 15 V et U1 = +7,5 V Lors du retour à de U'e à 0 V, U1 -U'e>0 : U2 = + 15 V. Étude de l’étage 3. Comment s’appelle la partie du montage ne comportant que l’amplificateur opérationnel et les fils qui l’entourent ? Suiveur de tension U3 = US. Montrer que si U2 = -15 V, alors US=0, et que si U2 =+15 V, alors US = +15 V. Si U2 = +15 V, la diode est passante et la tension aux bornes de la diode est nulle : U2 =U3 = US = +15 V. Si U2 = -15 V, la diode est bloquée et l'intensité qui travers la diode et R3 est nulle : U3 = US = 0 V.

retour -menu