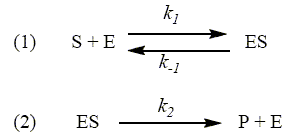Fermentation du glucose : solution tampon, catalyse enzymatique, chimie concours Mines 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Préparation du tampon phosphate. On désire préparer une solution tampon de pH égal à 6,2 et de concentration totale en phosphore égale à c = 0,10 mol.L-1. Pour cela, on utilise du dihydrogénophosphate de sodium hydraté NaH2PO4, 12 H2O (masse molaire M1 = 336 g.mol-1). Dans une fiole jaugée de volume V = 1,0 L, on verse de l’eau distillée puis on introduit une masse m1 de dihydrogénophosphate de sodium hydraté, on mélange. On ajoute une masse m2 d’hydroxyde de sodium NaOH (masse molaire M2 = 40 g.mol-1) et l’on complète au trait de jauge avec de l’eau distillée. Calculer la quantité m1 à introduire pour obtenir une solution de concentration totale en phosphore égale à c = 0,10 mol.L-1. m1 = 336*0,1 = 33,6 g. Quelles sont les espèces de H3PO4 présentes dans la solution tampon à ce pH ? Justifier. à pH = 6,2, H2PO4- et HPO42- prédominent. Écrire l’équation de la réaction qui se produit lorsqu’on ajoute l’hydroxyde de sodium. Calculer sa constante et conclure. Couples acide / base : H2PO4- / HPO42- ; H2O / HO-. H2PO4- + HO- = HPO42- +H2O avec K = [HPO42-] /([H2PO4-] [HO-]) Or : Ka2 = 10-7,2 = [HPO42-] [H3O+] / [H2PO4-] et Ke =[H3O+] [HO-] = 10-14. par suite K = Ka2 /Ke =10-7,2 /10-14 = 106,8 = 6,3 106, valeur importante, la réaction est totale.   Exprimer les concentrations en H2PO4- et HPO42- en fonction des quantités de matière n1 et n2 en H2PO4 et NaOH respectivement introduites et du volume V. n1 = m1 / M1 V = 0,1 mol ; n2 = m2 / M2 V = m2 / M2 ; avancement (mol) H2PO4- + HO- = HPO42- +H2O initial 0 n1 n2 0 solvant en large excès fin x n1-x n2 -x x l'hydroxyde de sodium est en défaut : n2 -x = 0 ; x = n2 [HPO42-] = n2 / V ; [H2PO4- ] =(n1-n2 )/ V Exprimer le pH de la solution en fonction de n1, n2 et de la (des) constante(s) d’acidité concernée(s). Ka2 = 10-7,2 = [HPO42-] [H3O+] / [H2PO4-] = n2[H3O+] / (n1-n2 ) log Ka2 = log [H3O+] + log ( n2 / (n1-n2 )) ; pKa2 =pH - log ( n2 / (n1-n2 )) ; pH = pKa2 +log ( n2 / (n1-n2 )). En déduire les valeurs de n2 puis de m2 à ajouter pour obtenir un pH égal à 6,2. 6,2= 7,2 + log(n2/(0,1-n2)) ; 1= log((0,1-n2)/n2) ; 10 = (0,1-n2)/n2 ; n2 = 0,1/11 =9,1 10-3 mol. m2 = M2 n2 = 40 * 9,1 10-3 = 0,36 g. Étude théorique de la catalyse enzymatique. Le mécanisme de réaction avec l’action de la levure peut être modélisé par la catalyse enzymatique. On considère la réaction S (substrat) = P (produit) catalysée par l’enzyme E et on admet que le mécanisme est le suivant : L’espèce notée ES est appelé complexe enzyme substrat. D’après le mécanisme proposé ci-dessus, exprimer v, la vitesse de formation du produit P. v d[P]/dt = k2 [ES] En notant [E]0 la valeur initiale de la concentration en enzyme, écrire l’équation traduisant la conservation totale de l’enzyme au cours de la réaction. [E]0 = [E] + [ES] Appliquer l’approximation des états quasi-stationnaires au complexe enzyme-substrat. En utilisant la question précédente, en déduire une expression de la concentration en complexe enzyme substrat en fonction de [E]0, [S] et des constantes. d[ES]/dt = k1[S][E]-k-1[ES]- k2 [ES] =0 ; [E] =(k-1 +k2 ) [ES] / ( k1[S] ) [E]0 = [E] + [ES] conduit à : [E]0 =(k-1 +k2 ) [ES] / ( k1[S] ) + [ES] = ((k-1 +k2 )/ ( k1[S] ) +1) [ES] [ES] =[E]0 / ((k-1 +k2 )/ ( k1[S] ) +1). On appelle constante de Michaelis et on note KM, l’expression KM=(k-1 +k2 )/k1. Exprimer alors v en fonction de [E]0, KM, k2 et [S]. [ES] =[E]0 / (KM/ [S] +1) ; v = k2[ES] =k2[E]0 / (KM/ [S] +1). Si la concentration en substrat augmente (à concentration initiale en enzyme constante), [S] devient bien supérieur à KM ; l’expression de la vitesse tend vers k2[E]0. C'est la vitesse maximale, vmax =k2[E]0. 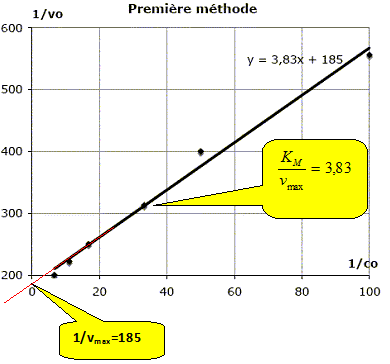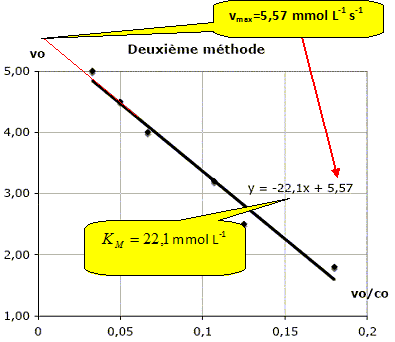L’expression de la vitesse obtenue ci-dessus permet de construire deux modèles. Ces modèles permettent de tracer des courbes qui deviennent des droites lorsqu’ils sont validés. Exprimer 1/v et montrer qu’en traçant 1/v en fonction de 1/[S], on peut valider le modèle. 1/v =KM/(k2[E]0) * 1/[S] +1/(k2[E]0) ; 1/v = KM /vmax *1/[S] + 1/vmax ; il s'agit de l'équation d'une droite de pente KM /vmax et d'ordonnée à l'origine 1/vmax. Monter que l’expression de la vitesse peut se mettre sous la forme : v=vmax-KMv /[S]. Montrer alors qu’en traçant v en fonction de v/ [S], on peut également valider le modèle. v = k2[E]0 / (KM/ [S] +1) =vmax /(KM/ [S] +1) ; v(KM/ [S] +1) =vmax. v +KMv / [S]=vmax ; v =vmax -KMv / [S]. v = f(v / [S]) : droite de pente -KM et d'ordonnée à l'origine vmax. Étude expérimentale. La méthode utilisée consiste à étudier différents systèmes en faisant varier la quantité initiale de substrat (ici le glucose) et en déterminant les vitesses initiales d’apparition du produit (ici l’éthanol gazeux). Comment détermine-t-on pratiquement, la vitesse initiale de la réaction étudiée ici ? Tracer la courbe d'équation [ éthanol] en fonction du temps ; le coefficient directeur de la tangente à t=0 est égal à la vitesse initiale. On a réalisé la conversion du glucose à 39 °C et obtenu les résultats suivants : v0(mmol L-1 s-1) 1,80 2,50 3,20 4,00 4,50 5,00 c0( glucose mmol L-1) 10,0 20,0 30,0 60,0 90,0 150 1/v0(mol-1 L s) 556 400 313 250 222 200 1/c0( glucose mol-1 L) 100 50,0 33,3 16,7 11,1 6,67 v0 /c0 (s-1) 0,18 0,125 0,107 0,0667 0,05 0,033 Les deux courbes obtenues sont données ci-dessous.   À partir de la première méthode, déterminer les valeurs de KM et vmax à 39 °C pour cette réaction.   vmax = 1/185 = 5,4 10-3 mol L-1 s-1 ; KM =3,83 vmax =3,83*5,4 10-3 =2,1 10-2 mol L-1. À partir de la deuxième méthode, déterminer les valeurs de KM et vmax à 39 °C. vmax = 5,57 mmol L-1 s-1 = 5,57 10-3 mol L-1 s-1 ; KM =22,1 mmol L-1 =2,1 10-2 mol L-1. Les résultats des deux méthodes sont compatibles.

retour -menu