cinétique d'oxydation : ion iodure et ion fer (III), chimie concours Mines 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Les couples mis en jeu sont I2 / I– et Fe3+ / Fe2+ (toutes espèces dissoutes dans l’eau). Écrire l’équation bilan de l’oxydation des ions iodure par les ions fer(III), en affectant les espèces du fer du coefficient stoechiométrique 1. I- = ½I2 + e- : oxydation ; Fe3+ + e- = Fe2+ : réduction Fe3+ + I- = ½I2 + Fe2+. Si la concentration d’ions iodure passe de c0 à c0 – x entre 0 et t, on définit par rapport à x la vitesse volumique v de la réaction de la manière suivante : v = -d[I-]dt = dx/dt. On suppose une cinétique avec ordre, de constante de vitesse k ; on note a l’ordre partiel par rapport aux ions fer(III) et b l’ordre partiel par rapport aux ions iodure. Comment s’écrit la vitesse v ? Quelle est alors l’unité usuelle de k (au besoin en fonction de a et b) ? v = k[Fe3+]a[I-]b avec v en mol L-1 s-1et les concentrations en mol L-1. [k ]= mol L-1 s-1 mol-(a+b) La+b = mol-(a+b)+1 La+b-1 s-1. A la date t après le mélange d’une solution d’iodure de potassium avec une solution ferrique, on prélève à la pipette 5 mL de solution et on le dilue 10 fois avant de procéder à un dosage de la quantité d’iode formée. Justifier l’intérêt cinétique de cette dilution. En diluant on divise laes concentrations des réactifs par 10 : or les concentrations des réactifs sont un facteur cinétique ; la vitesse de la réaction est divisée par 10a+b. On réalise ainsi un blocage cinétique. Les résultats d’une série de mesures sont présentés ci-dessous, x se rapportant à la quantité d’ions iodure qui ont été oxydés dans le milieu réactionnel à la date du prélèvement. t(s) 60 120 180 240 300 x(µmol/L) 13 25 36 46 55 Que représente la grandeur x(t) / t ? Pourquoi diminue-t-elle en cours de réaction ? 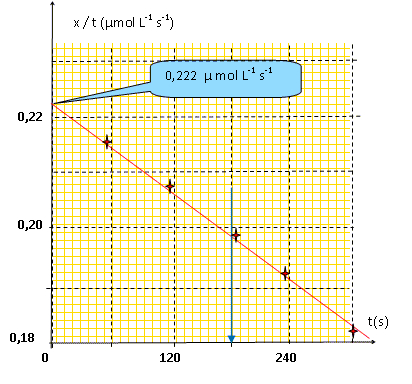x(t) / t représente la vitesse moyenne de la réaction entre deux dates t2-t1 : les concentrations des réactifs diminuent au cours de la réaction : la vitesse diminue. Représenter graphiquement la grandeur x(t)/t en fonction de t ; en déduire une estimation de la valeur initiale (dx/dt)0. t(s) 60 120 180 240 300 x / t (µmol L-1 s-1 ) 0,216 0,208 0,200 0,192 0,183 Grâce à la méthode précédente, on détermine les valeurs initiales de (dx/dt)0 pour différentes concentrations initiales des deux réactifs. Quelques résultats sont présentés ci-dessous : c0=[I-]0 µmol L-1 2 2 2 6 6 8 [Fe3+]0 µmol L-1 2 4 8 2 4 8 [dx/dt]0 µmol L-1 s-1 5,7 11,1 22,5 52 99 354 En déduire les valeurs de a et b, supposées entières. [dx/dt]0 = k[Fe3+]0a[I-]0b ; [I-]0 constante, si [Fe3+]0 double alors [dx/dt]0 double ; si [Fe3+]0 triple alors [dx/dt]0 triple : [dx/dt]0 et [Fe3+]0 sont proportionnelles ; a=1. [Fe3+] 0 constante, si [I-]0 est multipliée par 3, alors [dx/dt]0 est multipliée par 52/5,7 =9 ; si [I-]0 est multipliée par 4, alors [dx/dt]0 est multipliée par 354/22,5 ~ 16 d'où b = 2. v = k[Fe3+] [I-]02. Déterminer la valeur de la constante de vitesse k définie ci-dessus ; on précisera la méthode suivie pour utiliser au mieux les données. c0=[I-]0 mol L-1 2 10-6 2 10-6 2 10-6 6 10-6 6 10-6 8 10-6 [Fe3+]0 mol L-1 2 10-6 4 10-6 8 10-6 2 10-6 4 10-6 8 10-6 [dx/dt]0 mol L-1 s-1 5,7 10-6 11,1 10-6 22,5 10-6 5,2 10-5 9,9 10-5 3,54 10-4 k mol-2 L2 s-1. 7,1 1011 6,9 1011 7,0 1011 7,2 1011 6,9 1011 6,9 1011 k = [dx/dt]0 / ([Fe3+] [I-]02) = 7,0 1011 mol-2 L2 s-1. Dans l’hypothèse d’un état initial ne contenant que les deux réactifs à la même concentration c0, établir la relation littérale donnant x(t), sous la forme : « expression en (x,c0) = expression en (k,t) ». dx/dt = k (c0-x) (c0-x)2 ; dx / (c0-x)3 = kdt Intégrer : 1/(2(c0-x)2 )= kt + cste. à t=0, x=0 d'où : 1/(2c02 ) = cste. 1/(c0-x)2 -1/c02 = 2kt. En déduire la dépendance entre le temps de demi-réaction t et la concentration c0. Au temps de demi-réaction, x = ½c0 d'où : 1/(½c0)2 -1/c02 = 2kt. 3/c02 = 2kt ; t = 3/(2kc02 ).

retour -menu