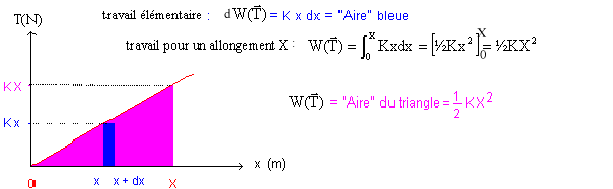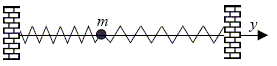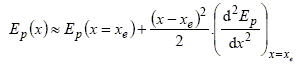Energie potentielle : modélisation d’un oscillateur physique concours Mines 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Soit un point matériel de masse m, en mouvement dans le champ de pesanteur g uniforme. Les caractères gras, écrits en rouge, désignent des grandeurs vectorielles. Étude énergétique d’un oscillateur. Définir l’énergie potentielle associée à une force F. L'énergie potentielle d'un système physique est associée à une force dite conservative : une force conservative dérive d'une énergie potentielle : F= - dEp/dr. L'énergie potentielle est définie à une constante près ; la variation d'énergie potentielle est l'opposé du travail W d'une force conservative. Pour une force de rappel élastique de constante K, déterminer l’expression de l’énergie potentielle en fonction de l’écart x à la position d’équilibre, à une constante additive près. La tension T est proportionnelle à l'allongement x du ressort T= K x K raideur du ressort (N/m) On considère un mouvement conservatif de m sur l’axe horizontal Oy, autour d’une position d’équilibre Y0, avec l’énergie potentielle Ep(y) = E0 + a ( y-Y0)2, où a est une constante positive. Établir l’équation différentielle du mouvement et en déduire qu’il s’agit d’oscillations harmoniques dont on précisera l’expression de la période. Expression de l'énergie mécanique : Em = Ep(y) + Ec(y) = E0 + a ( y-Y0)2 + ½ m(dy/dt)2 = constante. Dériver par rapport au temps : 2a ( y-Y0) dy/dt + m dy /dt . d2y /dt 2 = 0 Simplifier par dy/dt : 2a ( y-Y0) + m d2y /dt 2 = 0 ; d2y /dt 2 + 2a / m y = 2a / m Y0. C'est l'équation différentielle d'un oscillateur harmonique de pulsation w= (2a / m)½ et de période T = 2 p / w =2 p ( m/(2a) )½. 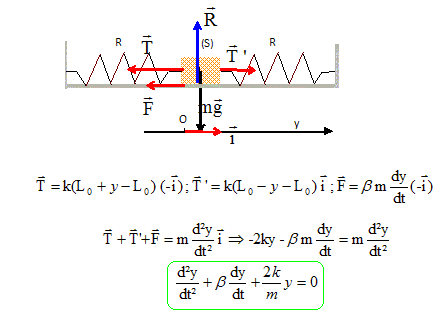Les ressorts sont identiques, de raideur k et de longueur à vide L0, tandis que les points d’attache sont distants de 2L0. Exprimer Ep(y) si y désigne l’écart à la position d’équilibre, et calculer la période T0 des oscillations de m si m = 200 g et k = 40 N/m. Les énergies potentielles ½ky2 + Cte de chaque ressort s'ajoutent ; si on choisit la position d'équilibre comme origine de l'énergie potentielle, la constante est nulle. Ep(y ) = ½ky2 +½ky2 = ky2 . On retrouve le cas précédent avec Y0 = 0 et a = k : T0 =2 p ( m/(2k) )½ = 6,28 (0,2/80)½ =0,31 s. On envisage l’existence d’un frottement fluide d’intensité proportionnelle à la vitesse de m par rapport à l’axe du mouvement : F = -ß m v, où ß est une constante. Donner la dimension ou l’unité SI de ß. ß = -F / (mv) : force : masse * accélération = masse * longueur / temps2 soit MLT-2. mv : masse * longueur / temps soit MLT-1 ; par suite [ß] = T-1. Établir l’équation différentielle du mouvement. Quelle est la valeur numérique maximale de ß permettant les oscillations de m ? Polynôme caractéristique : r2 +ßr +2k/m = 0 ; discriminant D = ß2 -8k/m. Le régime est pseudo-périodique si D <0 soit ß < 2 (2k/m)½ ; ß < 2 (80/ 0,2)½ ; ß < 40 s-1. 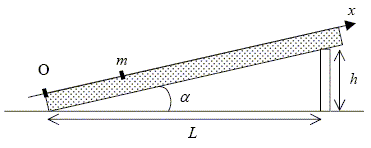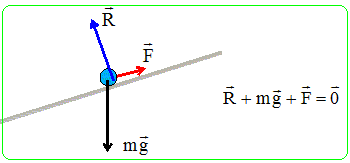Modélisation d’un dispositif expérimental. On dispose d’un banc à coussin d’air rectiligne (Ox), incliné par une cale de hauteur h d’un angle a par rapport à l’horizontale, selon la figure ci-dessous. Sur ce banc, un aimant est fixé à l’origine O, et un autre aimant, de masse m, est fixé sur un palet mobile sans frottement : Les aimants sont orientés de telle sorte qu’ils se repoussent mutuellement. La possibilité pour m d’osciller autour d’une position d’équilibre résulte de la compétition entre la répulsion électromagnétique, réduite à une force notée F, prépondérante lorsque les aimants sont proches, et le poids, qui devient prépondérant lorsque la distance augmente. Faire un bilan des forces à l’équilibre sur un schéma. Sans connaissances préalables en électromagnétisme, on cherche dans la suite à vérifier si la force électromagnétique agissant dans cette expérience peut être modélisée par une loi de la forme : F(x) = k.(x0 / x)n.ex, avec k > 0 et n entier naturel. Exprimer dans cette hypothèse la position d’équilibre xe en fonction de x0, k, m, g, L, h et n dans le cas des petits angles (h << L). NB : cette approximation sera toujours utilisée dans la suite. Projection sur Ox de la somme vectorielle des forces : -mg sin a + F = 0 sin a~ h/L ; mgh/L = k.(x0 / xe)n ; (mgh / (kL)) 1/n = x0 / xe ; xe = x0 . [kL / (mgh)] 1/n. On mesure xe pour différentes cales, puis on représente ln(h) en fonction de ln(xe / x0). En prenant x0 = 1 m, déduire des mesures ainsi représentées ci-dessous les valeurs de n et de k. On donne : L = 120 cm ; m = 189 g ; g = 9,81 m.s–2. ln(h) -2,19 -2,39 -2,56 -2,63 -2,73 -2,76 -2,81 ln(xe/x0) -4,61 -3,91 -3,22 -2,81 -2,53 -2,30 -2,12 mgh/L = k.(x0 / xe)n ; ln h + ln (mg/(kL)) = n ln (x0 / xe) = - n ln(xe / x0) coefficient directeur de la droite : -n = -(4,61-2,12) / (2,81-2,19) = - 4 ; n = 4. ln k = ln(mgh/L) +n ln(xe / x0) = ln (0,189*9,8 /1,2) + ln h + 4 ln (xe / x0) ln k = 0,435 + ln h + 4 ln (xe / x0) ln(h) -2,19 -2,39 -2,56 -2,63 -2,73 -2,76 -2,81 ln(xe/x0) -4,61 -3,91 -3,22 -2,81 -2,53 -2,30 -2,12 ln k -20,1 -17,6 -15,0 -13,4 -12,4 -11,5 -10,9 k est de l'ordre de 10-6 N m-1. Exprimer littéralement l’énergie potentielle totale Ep(x) de m, à une constante additive près, en fonction de x, x0, k, m, g, L, h et n, puis en fonction de x, x0, xe, k et n. Energie potentielle de pesanteur : Epp = mg x sin a + constante = mg x h/L + Constante. Energie potentielle magnétique : chercher une primitive de F = k.(x0 / x)n soit : 1/(n+1) k.x0n . x-n+1 / (n-1) Energie potentielle totale : Ep(x)= mg x h/L + k.x0n . x1-n / (n-1) +Constante. 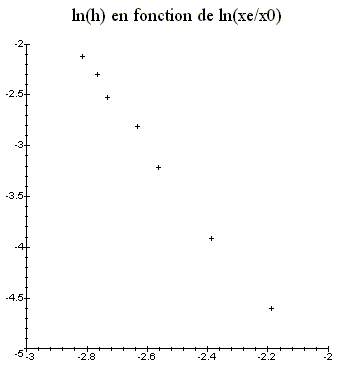Lorsqu’on se limite à des oscillations de faible amplitude autour de la position d’équilibre, on rappelle qu’on peut utiliser pour l’énergie potentielle un développement de Taylor d’ordre 2 : En déduire une expression de Ep( x~ xe) sous la forme : ½K(x-xe)2 + Cste ; on exprimera la constante K en fonction de xe, x0, k et n. K : valeur de la dérivée seconde de l'énergie potentielle pour x = xe. K = n k x0n. xe-1-n. Justifier qu’au voisinage de l’équilibre, la résultante des forces subies par m équivaut à une force de rappel élastique dont on précisera la constante de raideur équivalente. Ep( x~ xe) = ½K(x-xe)2 + Cste F = -dEp/dx = -K (x-xe). Toutes choses égales par ailleurs, montrer que la période T des petites oscillations autour de l’équilibre est proportionnelle à une puissance de h que l’on déterminera ; en déduire une méthode de mesure de n que l’on décrira succinctement. T2=4 p2 m /K ; K = n kx0n. xe-1-n ; m/K = m xen+1 / (n kx0n) Or xe = x0 . [kL / (mgh)] 1/n d'où : m/K = x0 m [kL / (mgh)](n+1)/n / (n kx0) = Cste . h -(n+1)/n. Par suite T = Cste . h -(n+1)/(2n) ; ln T = ln cste - (n+1) / (2n) ln h Mesurer la période pour différentes valeurs de h puis tracer la fonction lnT = f(ln h) : droite de pente - (n+1) / (2n) =-5/8.

retour -menu