Electrocinétique : circuit inductif, filtre RC passe bas physique concours Mines 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

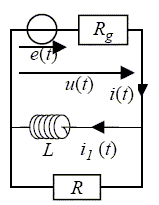
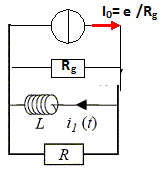
Modélisation linéaire d’un circuit. Le circuit ci-dessous est alimenté par un générateur dit « de Thévenin », dipôle actif linéaire de résistance interne Rg et de force électromotrice e(t). Donner le schéma équivalent ainsi que les grandeurs caractéristiques du générateur linéaire « de Norton » équivalent entre les mêmes bornes. Dans ce circuit, l’intensité i(t) fournie par le générateur se divise entre une inductance pure L (qui représente une bobine de résistance négligeable) et un résistor (résistance R). En respectant les notations du schéma, donner trois expressions de u(t) en régime quelconque, en fonction de i(t), i1(t) et des données. Branche contenant le générateur : u(t) = e(t) -Rg i(t). Branche contenant la bobine inductive : u(t) = Ldi1(t) /dt. Branche contenant le résistor : u(t) =R [i(t)-i1(t)]. La tension e(-oo < t < 0) est égale a une valeur constante notée E ; déterminer rapidement la tension u(t = 0-) ainsi que les intensités i(t = 0-) et i1(t = 0-). u(t = 0-) = E- Rg i(t= 0-) La bobine inductive a stocké un maximum d'énergie : l'intensité i1(t= 0-) est constante, le régime permanent est atteint. di1(t = 0-) /dt =0 ; en conséquence u(t = 0-) =Ldi1(t = 0-) /dt =0. u(t= 0-) =R [i(t= 0-)-i1(t= 0-)] =0 ; i(t= 0-)=i1(t= 0-). E- Rg i(t= 0-) = 0 ; i(t= 0-) =E/Rg. A t = 0, on « éteint » le générateur, qui devient équivalent à sa seule résistance interne (ce qui signifie qu’on a e(t > 0) = 0) ; établir l’équation différentielle régissant l’évolution ultérieure de u(t), et faire apparaître la constante de temps t du circuit. Résistance équivalente à Rg et R montées en dérivation : Réqui = RRg / (R+Rg). u(t) = Ldi1/dt = -Réqui i1(t) ; i1(t) = -u(t) / Réqui ; di1/dt = -1/Réqui du(t)/dt. par suite u(t) = -L/Réqui du(t)/dt. du(t)/dt + Réqui/ L u(t) = 0 ; t = L/Réqui. du(t)/dt + 1/ t u(t) = 0 (1). 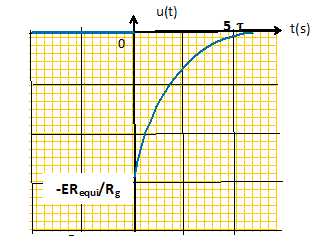En utilisant une propriété remarquable d’une grandeur – propriété à préciser, déterminer u(t = 0+). La continuité de l'énergie impose la continuité de l'intensité du courant dans la bobine : i1(t= 0+) =E/Rg. u(t = 0+) = -Réqui i1(t= 0+) = - RéquiE/Rg. ( discontinuité de la tension aux bornes de la bobine). Déterminer complètement u(t > 0) puis donner l’allure de la représentation graphique de u pour t compris entre -10 t et + 10 t. Solution générale de (1) : u(t) = A exp(-t / t ) avec A une constante. u(t=0+) =A = - RéquiE/Rg. u(t) = - RéquiE/Rg exp(-t / t ). Générateur et oscilloscope. On s’intéresse à quelques caractéristiques de ces deux appareils essentiels. On dispose d’un voltmètre de très grande résistance interne (considérée infinie), d’un générateur de tension (GBF) et de boîtes de résistances réglables. La force électromotrice du générateur étant fixée (en continu), on effectue entre ses bornes les deux mesures suivantes : mesure (1) : on mesure une tension U = 6 V pour une résistance de charge infinie ; mesure (2) : on mesure une tension de 3 V pour une charge égale à 50 ohms. Déduire de ces mesures la résistance interne Rg et la force électromotrice E du générateur étudié. Pour une résistance de charge infinie, l'intensité du courant est nulle : la mesure (1) donne la f.e.m E du générateur : E = 6 V. mesure (2) : u = E-Rg i = R i ; i = u/R ; u = E-Rg/R u ; 1 = E/u -Rg/R ; Rg= (E/u-1) R Rg=(6/3-1)*50 = 50 ohms. 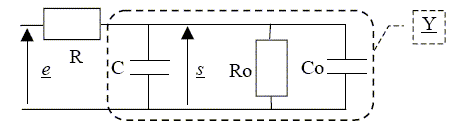On alimente désormais par ce générateur une association R-C série, en régime sinusoïdal de pulsation w réglable. Quelle sera, en module, l’impédance de charge minimale du générateur ? A quelle condition (qualitative) pourra-t-on considérer le générateur comme idéal ? Impédance complexe du dipôle R-C série : Z = R+1/(jCw) = (1+jRCw) /(jCw) = (j-RCw) /(Cw) Module de Z : [1+(RCw)2]½ / (Cw) = [1/(Cw)2 +R2]½. L'impédance de charge est minimale pour une pulsation w très grande. Zmini = R. Le générateur peut être considéré comme idéal si sa résistance interne Rg est très inférieure à la résistance minimale de charge. On supposera cette condition remplie dans la suite, avec R = 4,7 kiloohms et C = 22 nF. En l’absence d’oscilloscope branché sur le circuit, déterminer la fonction de transfert complexe en tension H si la grandeur de sortie est la tension aux bornes du condensateur ; quel est le filtrage ainsi réalisé ? Comment définit-on la pulsation de coupure wC d’un filtre de cette nature et comment s’exprime-t-elle ici ? Application numérique : calculer la fréquence de coupure du filtre. H = 1/(jCw Z) =1 /(1+jRCw). On pose w0 =1/(RC) et x =w /w0 ; H = 1/(1+jx) Module de H : H = (1+x2)-½ ; gain : GdB = 20 log H = -10 log(1+x2). Il s'agit d'un filtre passe bas. Coupure à - 3 dB : -3 = -10 log (1+x2) ; 1+x2 = 2 ; x = 1 ; wC = w0. wC =1/(RC) = 1/(4700*22 10-9) =9,7 103 rad/s ; fC = wC /(2 pi) =1,5 103 Hz. On utilise un oscilloscope dont les caractéristiques d’entrée sont indiquées :" 106 ohms, 25 pF". Dans la suite, on désigne par R0 et C0 la résistance et la capacité correspondantes. Cet appareil, branché sur le filtre précédent, correspond ainsi au circuit suivant : Déterminer simplement le gain en tension à basse fréquence, noté H0. A basse fréquence, un condensateur se comporte comme un interrupteur ouvert. Admitance d'entrée de l'oscilloscope : Y = jC0w + 1/R0 à basse fréquence : Y0 =1/R0 ; Z0 = R0. H0 = s / e = R0/ (R+R0). Exprimer l’admittance complexe Y. Y = j(C+C0)w + 1/R0 = [ jR0(C+C0)w + 1] /R0. Quelle est la limite à basse fréquence du déphasage de la tension s par rapport à l’intensité i parcourant le dipôle équivalent d’admittance Y ? i = Y s ; arg i = arg Y + arg s ; en choisissant arg i = 0, arg s = -arg Y = - R0(C+C0)w. Quand w tend vers zéro, arg s tend vers zéro. Le déphasage de la tension s par rapport à l’intensité i tend vers zéro. Déterminer la nouvelle fonction de transfert H’ = s / e sous la forme H0/ (1+jw /w0). Z' = 1/ Y = R0 / [ jR0(C+C0)w + 1] ; s / e = Z' / (Z' +R)= 1/ (1+R/Z') = 1/(1+RY) = 1 / (1+R[ jR0(C+C0)w + 1] /R0 ). s / e =R0 / [R0+R + jRR0(C+C0)w] = R0 / (R0+R) *1 / [ 1 + jRR0(C+C0)w/ (R0+R)] On pose w0 = (R0+R) / [RR0(C+C0)] ; H' =R0 / (R0+R) *1 / (1 + jw /w0). H' ~H0 / (1 + jw /w0). w0 =(106+4700) / (106*4700 ( 22 10-9 +25 10-12)) =9,7,06 103 rad/s. f0 = 9,081 103 /6,28 =1,55 103 Hz. La fréquence de coupure est pratiquement inchangée : l'oscilloscope est approprié pour l'étude du flitre passe bas.

retour -menu