Charge et décharge d'un condensateur ( dipôle RC) concours ENI GEIPI 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

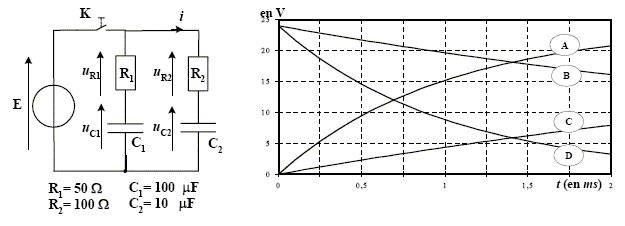
A l’instant t = 0, on ferme l’interrupteur K durant une durée t0 = 2 ms. On charge alors 2 condensateurs idéaux (sans résistance de fuite) à l’aide d’un générateur de tension E. On enregistre les 4 courbes ci-dessous. Relier les tensions uR1, uC1, uR2, uC2 à leurs courbes respectives. Constante de temps R1C1 = 50 * 100 10-6 = 5 10-3 s = 5 ms. Constante de temps R2C2 = 100 * 10 10-6 = 1 10-3 s = 1 ms. La tension aux bornes d'un condensateur est croissante : la charge est pratiquement terminée au bout d'une durée proche de 5 fois la constante de temps, d'où : A : uC2 ( durée de la charge ~ 5 ms) C : uC1 ( durée de la charge ~ 25 ms) La tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles. uR1 = R1 i1 = 50 i1 ; uR2 = R2 i2 = 100 i2. Lors de la charge d'un condensateur à travers un résistor, l'intensité est décroissante i = Imax exp(-t/(RC)) ; i1(2) = Imax exp(-2/5) = 0,67 Imax ; i2(2) = Imax exp(-2/1) = 0,14 Imax . uR1 =50*0,67 Imax ; uR2 =100*0,14 Imax d'où : B : uR1 ; D : uR2. Déterminer la valeur de la tension E. uR1 (0) = 24 = R1 Imax = avec Imax = E/R1. uR1 (0) =E = 24 V. ( lecture graphe à t=0) A t0 = 2 ms, calculer : l’énergie Ec1 emmagasinée par le condensateur C1. Ec1 = ½C1u2C1 avec uC1 = E(1- exp(-2/5) =7,9 V Ec1 =0,5*10-4*7,92 =3,1 10-3 J. l’énergie Ec2 emmagasinée par le condensateur C2. Ec2 = ½C2u2C2 avec uC2 = E(1- exp(-2/1) =20,1 V Ec2 =0,5*10-5*20,12 =2,2 10-3 J. la charge Q1 portée par l’armature positive de C1, Q1 = C1 uC1 =7,9 10-4 C. la charge Q2 portée par l’armature positive de C2, Q2 = C2 uC2 =2,0 10-4 C. A l’instant t = t0, on ouvre l’interrupteur K. On s’intéresse au régime permanent qui s’installe ensuite. Comment va évoluer la charge totale QT portée par les 2 condensateurs ? La charge totale reste constante ( conservation de la charge) Si on note Q1, respectivement Q2, la charge des condensateurs de capacité C1, respectivement C2 à la date t0 : QT = Q1 + Q2.  On mesure l’intensité du courant i(t) pour t > t1 = 100 ms ; on constate qu’elle est nulle. Pourquoi ? Le circuit est équivalent à un dipôle RC de : - résistance R = R1+R2 = 150 W. - capacité C = C1C2/(C1+C2 ) = 100*10/110 =9,09 µF - de constante de temps t = RC = 150 *9,09 10-6 = 1,36 10-3 s ~ 1,4 ms. Or i(t) est de la forme -Imax exp(-t/ t ) = -Imax exp(-100/ 1,4 ) ~ 0. L'intensité est nulle ( décharge d'un condensateur à travers un résistor) car t1 est très supérieur à la constante de temps : la décharge est donc terminée. Pourquoi a-t-on pour t > t1 : uC1= uC2 ? Additivité des tensions uC1 + uR1 = uC2 + uR2 uR1 = R1 i = 0 ; uR2 = R2 i = 0 ; d'où uC1= uC2. En déduire uC1 pour t > t1, en fonction de QT, C1 et C2. Q1 = C1 uC1 ; Q2= C2 uC2 ; Q1+Q2=QT et uC1= uC2 d'où : QT = (C1 + C2) uC1 ; uC1 = QT / (C1 + C2). A.N : uC1 = 9,9 10-4 /(1,1 10-4 )= 9 V. Calculer l’énergie totale EcT emmagasinée par C1 et C2 pour t = t1 et conclure. EcT = ½ C1u2C1 +½ C2u2C2 = ½(C1+C2)u2C1 ; EcT = ½(C1+C2)Q2T / (C1 + C2)2 = ½Q2T / (C1 + C2). EcT =0,5 *(9,9 10-4)2 / (1,1 10-4 )=4,5 10-3 J. Or à t = 2 ms : Ec1 + Ec2 = 5,3 10-3 J. Une partie de l'énergie initiale ( 0,8 mJ ) est perdue par effet Joule dans les conducteurs ohmiques lors de la déharge de l'un des condensateurs.

c

retour -menu