Euler, énergie mécanique, chute libre : physique concours FESIC 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Répondre par vrai ou faux. A la date t = 0, une population de noyaux radioactifs comporte N0= 1000 noyaux. On se propose de déterminer l’évolution du nombre de ces noyaux à l’aide de la méthode d’Euler. La constante radioactive est l = 0,1 s-1 et le pas choisi est Dt = 0,5 s. On donne dN/dt = -l N où dN/dt est la fonction dérivée de n(t) par rapport au temps.   A- L’évolution du nombre de noyaux se désintégrant est N(t) = N0 exp(-lt). Vrai. Loi de décroisance radioactive. B- Le nombre de noyaux restant à la date 0,5 s est de 950. Vrai. D N = -l N Dt et N(t+Dt) = N(t) + D N. D N = -l N Dt = -0,1*950*0,5 = 50 ; N(0,5) =N0 +D N = 1000-50 = 950. C- Le nombre de noyaux restant à la date 2 s est de 903. Faux. D N = -l N Dt = -0,1*1000*0,5 = -47,5 ; N(1) =N(0,5) +D N = 950-47,5 ~ 903. D- 185 noyaux se sont désintégrés à la date 2 s. Vrai. D N = -l N Dt = -0,1*903*0,5 = -45,1 ; N(1,5) =N(1) +D N = 903-45,1 ~ 858. D N = -l N Dt = -0,1*858*0,5 = -42,9 ; N(2) =N(1,5) +D N = 858-42,9 ~ 815. 1000-815 = 185. On néglige toutes les forces dues à l’air : la bille est en chute libre. 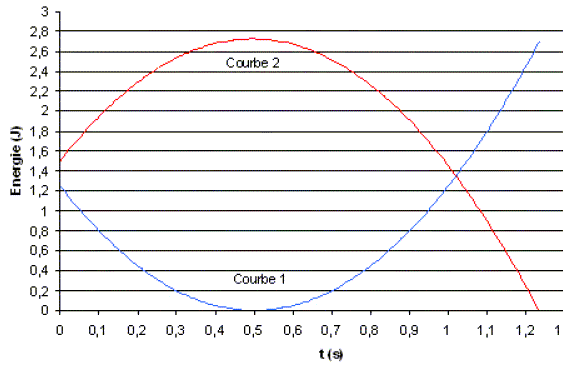Une bille de masse m = 100 g est lancée verticalement vers le haut avec une vitesse initiale v0 = 5,0 m.s-1. Grâce à un dispositif de chronophotographie, on a relevé l’altitude de la bille à intervalles de temps réguliers. On a pu ainsi tracer sa courbe d’énergie potentielle (origine choisie au niveau du sol) et sa courbe d’énergie cinétique en fonction du temps. Données : valeur du champ de pesanteur terrestre g = 10 m.s-2 ; 54½~7,4. A-La courbe 1 représente l’énergie potentielle de la bille. Faux. Epot = mgh ave h : altitude par rapport au sol. L'altitude de la bille augmente, atteint une valeur maximale, puis diminue : la courbe 2 traduit cette évolution. B- La bille a été lancée avec une énergie mécanique d’environ 2,7 J. Vrai. L'énergie mécanique se conserve : lorsque la vitesse est nulle, l'énergie mécanique est sous forme potentielle de pesanteur et vaut 2,7 J (valeur maximale lue sur la courbe 2) ) C- La bille a été lancée d’un point d’altitude h égale à 1,25 m. Faux. Conservation de l'énergie mécanique : 2,7 = ½mv02 + mg h avec m = 0,1 kg ; g = 10 m s-2 et v0 = 5 m/s. 2,7 = 0,5*0,1 *25 +0,1*10 h ; 2,7 = 1,25 +h ; h= 1,45 m. D- La bille retombe sur le sol avec une vitesse d’environ 7,4 m/s. Vrai. Conservation de l'énergie mécanique : 2,7 = ½mv2 + 0 ; v = (5,4 /0,1)½ = 54½~7,4. Dans un référentiel terrestre, on considère la chute d’un parachute de masse m = 20 kg portant une masse M. A l’instant initial, le parachute et sa charge sont abandonnés, sans vitesse initiale, d’une hauteur h = 320 m. On négligera la poussée d’Archimède. Le mouvement est étudié selon un axe vertical ascendant (Oz) dont l’origine O se situe sur le sol. La valeur du champ de pesanteur est : g = 10 m.s-2. Le parachute ne s’ouvre pas, la résistance de l’air est négligée. A- L’équation horaire du parachute chargé s’écrit : z = +5,0 t2. Faux. Le vecteur accélération est dirigé vers le bas, en sen contraire de l'axe : a =-g. Le vecteur vitesse est une primitive de l'accélération : v = -gt+ cte ; la vitesse initiale étant nulle, la constante d'intégration est nulle. v = -gt. Le vecteur position est une primitive du vecteur vitesse z = -½gt2 + cte ; l'altitude initiale vaut 320 m d'où : z = -½gt2 +320. B- Le parachute arrive au sol à la vitesse de 80 m.s-1. Vrai. Conservation de l'énergie mécanique ; mgh = ½mv2 ; v = (2gh )½ = (2*10*320 )½ =(64*100 )½ =80 m/s. Le parachute s’ouvre et la résistance de l’air R est proportionnelle au carré de la vitesse : R = kv2 avec k = 20 unités S.I. Le parachute et sa charge atteignent maintenant une vitesse limite de 7,0 m.s-1. C- La masse M vaut 78 kg. Vrai. La vitesse limite étant atteinte, le mouvement est rectiligne uniforme ; les forces se neutralisent. Le poids compense la résistance de l'air : (m+M)g = kv2 ; (20+M) *10 = 20*49 ; 20+M = 98 ; M = 78 kg. D- L’accélération est nulle. Vrai. La vitesse limite étant atteinte, le mouvement est rectiligne uniforme : la valeur de la vitesse est constante, l'accélération s'annule. On néglige toutes les forces dues à l’air. Deux élèves de terminale S réalisent une expérience : Pauline se trouve sur son balcon et lâche un ballon sans vitesse initiale. Agathe se trouve dans la rue et voit le ballon atteindre le sol 1,1 seconde plus tard. Données : Valeur du champ de pesanteur g = 10 m.s-2 ; 112 = 121 ; 1,2 / 5 = 0,24 ; 50½ = 7,1 ; 5½~2,23 ; 0,5½~0,71 A- le ballon a été lâché d’une hauteur h = 2,4 m. Faux. On choisit un axe vertical orienté vers le haut dont l'origine est le sol. Le vecteur accélération est dirigé vers le bas, en sen contraire de l'axe : a =-g. Le vecteur vitesse est une primitive de l'accélération : v = -gt+ cte ; la vitesse initiale étant nulle, la constante d'intégration est nulle. v = -gt. Le vecteur position est une primitive du vecteur vitesse z = -½gt2 + cte ; l'altitude initiale vaut h d'où : z = -½gt2 +h. Au sol z=0 ; h = ½gt2 = 0,5 *10*1,12 = 5*1,21~ 6,1 m. B- Le ballon heurte le sol avec une vitesse de 39,6 km/ h. Vrai. Valeur de la vitesse : v= gt = 10*1,1 = 11 m/s = 11*3,6 km/h = 39,6 km/h. Les deux élèves assistent ensuite à un spectacle de jonglage. D’une hauteur correspondant à sa stature, un jongleur lance verticalement une balle. Celle-ci atteint une altitude de 2,5 m par rapport au sol avant de redescendre. C- La vitesse initiale de la balle est inférieure à 7,1 m/s. Vrai. Conservation de l'énergie mécanique : mghmaxi = ½mv02 + mg h ; v0 = (2g(hmaxi -h))½ = (20(2,5-h))½ ; La valeur maximale de la vitesse initiale est obtenue pour h=0 soit vmax = 50½ =7,1 m/s. D- La balle a mis 0,71 s pour atteindre son altitude maximale. Faux. On choisit un axe vertical orienté vers le haut dont l'origine est le sol. Le vecteur accélération est dirigé vers le bas, en sen contraire de l'axe : a =-g. Le vecteur vitesse est une primitive de l'accélération : v = -gt + v0 . Au point le plus haut, la vitesse est nulle : 0 = -gt + v0 ; t = v0 /g Le temps est inférieur ou égal à 7,1/10 = 0,71 s.

retour -menu