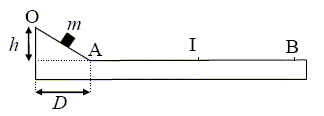Chute dans un fluide, équilibre d'un solide, accélération, travail d'une force : physique concours ESIEE 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

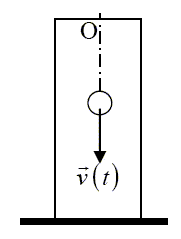
Répondre par vrai ou faux. Les vecteurs sont écrits en gras et en rouge. A l’instant t = 0 , on lâche à partir de O et sans vitesse initiale une bille de masse m pleine dans un fluide visqueux. Outre son poids mg , la bille est soumise à une force de frottement fluide du type -kv , où k est une constante et v le vecteur vitesse à l’instant t . La taille du récipient est supposée très grande. On néglige la poussée d’Archimède. 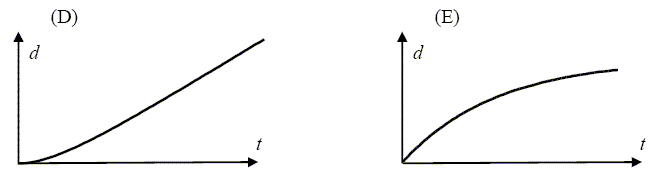A- A l’instant t = 0 , l’accélération de la bille est nulle. Faux. La vitesse initiale est nulle : la force de frottement fluide est donc nulle. La bille n'est soumise qu'à son poids, elle est alors en chute libre : l'accélération initiale est égale à g B- La vitesse de m tend vers vlim = mg /k lorsque le temps devient très grand. Vrai. Le poids et la force de frottement fluide se compense lorsque la vitesse limite est atteinte. mg = k vlim ; vlim =mg/k. C- La bille atteint ½vlim à l’instant t = (m ln 2)/ k. Vrai. La seconde loi de newton s'écrit sur un axe vertical orienté vers le bas : mg- kv = mdv/dt ; dv/dt + k/m v = g (1). Solution générale de dv/dt + k/m v =0 : v = A exp(-k/m t) Solution particulière de (1) : vlim =mg/k. Solution générale de (1) : v = A exp(-k/m t) +mg/k. A t=0, la vitesse est nulle : 0 = A +mg/k d'où a = -mg/k. v(t) = mg/k [ 1-exp(-k/m t)]. ½ vlim =0,5 mg/k = mg/k [ 1-exp(-k/m t)] ; 0,5 = 1-exp(-k/m t) ; 0,5 = exp(-k/m t) ln0,5 = -k/m t ; ln 2 = k/m t ; t = m ln2 / k. D- La distance parcourue par la bille en fonction du temps est de la forme : Vrai. E- Faux. Quand la vitesse limite est atteinte, le mouvement est uniforme : d = vlim t. Lâchée de O sans vitesse initiale, une masse m, supposée ponctuelle, parcourt d’abord une portion OA inclinée par rapport à l’axe horizontal puis aborde une portion horizontale à partir de A pour s’arrêter en B. m subit une force de frottement du type -Fu où F est une constante et u un vecteur unitaire colinéaire au vecteur vitesse de m à un instant t quelconque. On note g l’accélération de la pesanteur et I le milieu de [AB] . Données : m = 200 g ; h = 6 m ; AB = 50 m ; g =10 m.s-2 et la vitesse de passage en A est v =10 m s-1. A- F= 2 N . Faux. Travaux des forces entre A et B : - travail nul du poids, force perpendiculaire à la vitesse. - travail résistant de F : -AB * F = -50 F Variation de l'énergie cinétique : 0-½mv2 = -0,5*0,2 *102 = -10 J Théorème de l'énergie cinétique : -10 = -50 F ; F = 0,2 N. B- D= 8 m. Vrai. Travaux des forces entre O et A : - travail moteur du poids en descente : mgh = 0,2*10*6 = 12 J. - travail résistant de F : -OA * F = -0,2 OA. Variation de l'énergie cinétique : ½mv2 = 0,5*0,2 *102 = 10 J Théorème de l'énergie cinétique : 10 = 12-0,2 OA ; OA = 10 m. D2 = 102-h2 = 100-36 = 64 ; D= 8 m C- m parcourt OA en 1 seconde. Faux. Ecrire la seconde loi de Newton suivant OA : mg sin a -F = ma ; a = g sin a -F/m avec sin a = h/OA = 6/10 = 0,6. a = 10*0,6 -0,2 / 0,2 = 6-1 = 5 m s-2. v(t) = at = 5 t ; x(t) = 0,5 at2 = 0,5*5t2 =2,5 t2 ; 10 = 2,5 t2 ; t = 2 s. D- m parcourt AB en 10 secondes. Vrai. Ecrire la seconde loi de Newton suivant AB : -F = ma ; a = -F/m. a = -0,2 / 0,2 = -1 m s-2. v(t) = at +10 = - t ; x(t) = 0,5 at2 +10 t= -0,5t2 +10 t ; 50 = -0,5 t2 +10 t t2 -20 t+100 =0 ; delta = 400-400 =0 ; t = 10 s. E- m passe en I cinq secondes après son passage en A. Faux. x(t) = -0,5 t2 +10 t ; 25 = -0,5 t2 +10 t ; t2 -20 t +50 =0 ; delta = 400-200 = 200 ; 200½ ~14 ; t = (20-14) /2 ~3 s. 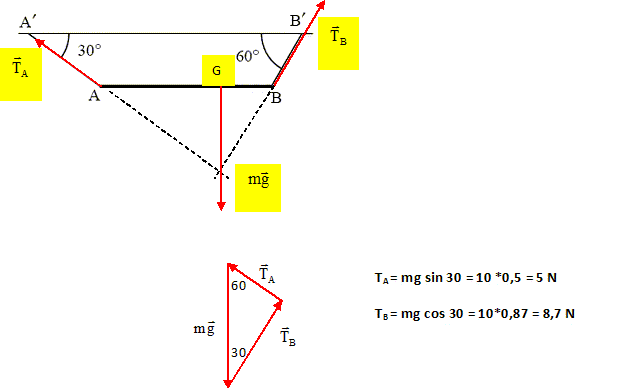Une barre non homogène AB, de poids P =10 N et d’un mètre de long, est fixée à un support horizontal A' B'. A l’équilibre, AB est horizontale et les fils tendus AA' et BB' font respectivement les angles 30° et 60° avec A'B'. On note TA la tension du fil AA' sur la barre et TB la tension du fil BB'. A- TA est dirigée de A' vers A. Faux. B- Le centre de gravité de la barre est plus proche de A que de B. Faux. C- TA <TB. Vrai. D- TA= 5 N. Vrai. E- TA+TB= 10 N. Faux. A l'équilibre la somme vectorielle des forces est nulle. En fonction des unités A (ampère), V (volt) et s (seconde) A- une résistance s'exprime en V A-1 . Vrai. R = U / I. B- la capacité d’un condensateur s’exprime en V-1A s. Vrai. C = q/U = I t / U C- l’inductance d’une bobine s’exprime en. V A-1 s. Vrai. tension aux bornes d'une bobine : U = Ldi/dt ; L = U dt / di. D- l’énergie s’exprime en V.A.s. Vrai. W = U I t. E- la puissance s’exprime en V.A. Vrai. P = U I. Un circuit, alimenté par un générateur de tension périodique, est constitué d’une résistance R = 60 ohms et d’une bobine d’inductance L supposée parfaite. On visualise les tensions uAM(t) et uBM(t). 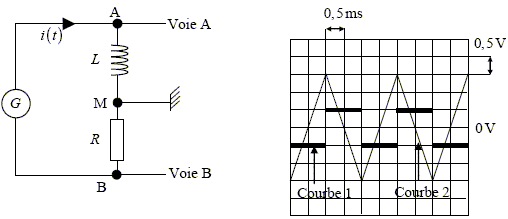A- La voie A correspond à la courbe 1. Vrai. On visualise la tension aux bornes de la bobine : uAM(t) = Ldi/dt. i(t) étant triangulaire, di/dt est constante par intervalle. B- La période du générateur vaut 2 ms. Vrai. 4 divisions soit 4*0,5 = 2 ms C- L = 0,02 H. Faux. Entre 0 et 1 ms, uBM(t) est croissante : uBM(t) = -R i(t) = -3/ 10-3 t ; 60 i(t) = -3 103 t ; i(t) = -3000/60 t = - 50 t. di/dt = -50 A s-1 ; uAM(t) = Ldi/dt = -0,5 V ; -50 L= -0,5 ; L = 0,5/50 = 0,01 H. D- L’intensité maximale vaut 25 mA. Vrai. valeur maximale de uBM(t) : 1,5 V ; valeur maximale de l'intensité : 1,5/60 = 1/40 = 0,025 A = 25 mA. E- L’énergie maximale emmagasinée par la bobine vaut 0,125 mJ. Faux. ½Li2 =0,5*0,01*(2,5 10-2)2 =3,1 10-6 J.

retour -menu