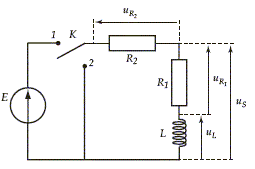
Circuit (RL), concours ingénieur EPF 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

On se propose d’´etudier le circuit RL suivant. Il est composé d’un générateur continu E, d’un interrupteur K, de deux réesistances R1 et R2 et d’une bobine L. Pour toute l’éetude on considère que la bobine a une résistance négligeable. L’interruteur est en position 1 depuis trèes longtemps. Précisez les adjectifs (permanent, transitoire, continu, alternatif) qualifiant le régime. Quelles sont les valeurs littérales de uL, i, uR1 , uR2 , uS en fonction de E, R1 et R2 ? Régime permanent ; le circuit est traversé par un courant continu, d'intensité constante égale à i = E/(R1+R2). L'intensité étant constante, sa dérivée par rapport au temps est nulle ; or uL = Ldi/dt ; donc uL = 0. uR1 = R1 i =R1 E/(R1+R2) ; uR2 = R2 i =R2 E/(R1+R2). uS = uR1 + uL =uR1 +0 = R1 E/(R1+R2). A t = 0 s, l’interrupteur est placé en position 2. En utilisant les résultats de la question 1, que vaut, au début du régime transitoire, i(t = 0+) ? En déduire les valeurs de uR1(t = 0+), uR2(t = 0+) ? puis uS(t = 0+) et uL(t = 0+). La continuité de l'énergie stockée par la bobine, donc la continuité de l'intensité conduit à : i(t = 0-) = i(t = 0+) = E/(R1+R2). uR1(t = 0+) =R1 i(t = 0+) =R1 E/(R1+R2) uR2(t = 0+) =R2 i(t = 0+) =R2 E/(R1+R2). 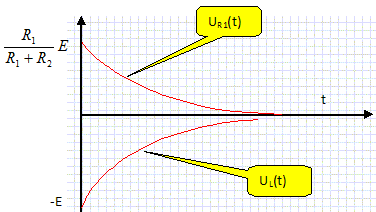Additivité des tensions : uR2(t = 0+) + uS(t = 0+) = 0 uS(t = 0+) = -uR2(t = 0+) = -R2 E/(R1+R2). Additivité des tensions : uR1(t = 0+) + uL(t = 0+) = uS(t = 0+) uL(t = 0+) = uS(t = 0+) -uR1(t = 0+) =-R2 E/(R1+R2) -R1 E/(R1+R2) ; uL(t = 0+) = -E. Ecrire l’équation différentielle régissant i(t) entre t =0+ et t --> +oo. Additivité des tensions : uR1 + uR2 + uL = 0 R1 i(t) + R2 i(t) + Ldi(t) / dt = 0 di(t) / dt + (R1 +R2 ) /L di(t) / dt = 0. Une solution de cette équation différentielle est de la forme i(t) = Aexp(-Bt). Déterminer A et B en utilisant les conditions initiales. i(t=0+) = A exp(0) = A = E/(R1+R2). di/dt = -AB exp(-Bt) u(t=0+) = -E = L[di/dt]t=0+ =-AB L exp(-0) = -AB L d'où B = E/(AL) ; B= (R1+R2) / L.  i(t) = E/(R1+R2) exp[ - (R1+R2) t / L ]. Donner les expressions littérales de uR1(t) et de uL(t). uR1(t) = R1 i(t) = R1E/(R1+R2) exp[ - (R1+R2) t / L ]. uL(t) = Ldi(t)/dt ; di(t) / dt = -E /L exp[ - (R1+R2) t / L ]. uL(t) = -E exp[ - (R1+R2) t / L ]. Tracer l’allure de uR1(t) et de uL(t) en précisant les valeurs pour t= 0+ et t--> +oo.

c

retour -menu